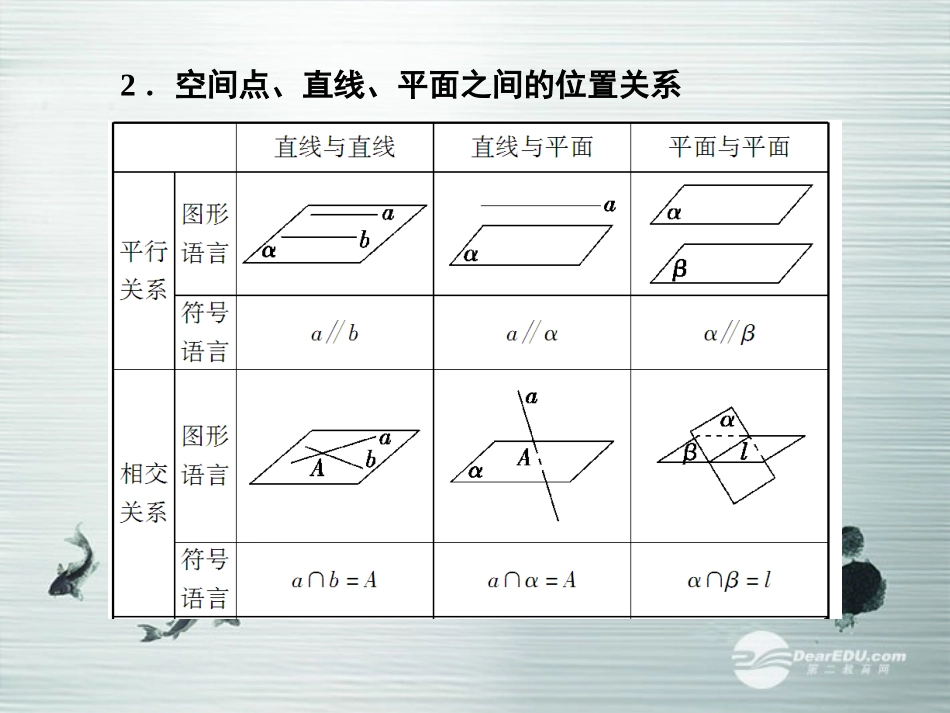
第三节空间点、直线、平面之间的位置关系1.平面的基本性质公理1:如果一条直线上的________在一个平面内,那么这条直线在这个平面内.公理2:过____________的三点,有且只有一个平面.公理3:如果两个不重合的平面有一个公共点,那么它们________________过该点的公共直线.两点不共线有且只有一条2.空间点、直线、平面之间的位置关系3.异面直线所成的角(1)定义:设a,b是两条异面直线,经过空间中任一点O作直线a′a∥,b′b∥,把a′与b′所成的___________叫做异面直线a与b所成的角.锐角或直角(2)范围:(0,π2].4.平行公理平行于同一条直线的两条直线________.5.空间角定理空间中如果两个角的两边分别对应平行,那么这两个角__________________.平行相等或互补1.若直线a平面α,直线b平面α,则直线a,b是异面直线,这种说法正确吗?【提示】此说法不正确,直线a,b都不在平面α内,但可能都在平面β内.2.若一条直线l不在平面α内,则直线l与平面α是否一定平行?【提示】不一定.直线l与平面α可能平行,也可能相交.1.(人教A版教材习题改编)下列命题正确的个数为()①梯形可以确定一个平面;②若两条直线和第三条直线所成的角相等,则这两条直线平行;③两两相交的三条直线最多可以确定三个平面;④如果两个平面有三个公共点,则这两个平面重合.A.0B.1C.2D.3【解析】②中两直线可以平行、相交或异面,④中若三个点在同一条直线上,则两个平面相交,①③正确.【答案】C2.已知a、b是异面直线,直线c∥直线a,那么c与b()A.一定是异面直线B.一定是相交直线C.不可能是平行直线D.不可能是相交直线【解析】若cb∥, ca∥,∴ab∥,与a,b异面矛盾.∴c,b不可能是平行直线.【答案】C3.(2013·佛山模拟)若直线l不平行于平面α,且lα,则()A.α内的所有直线与l异面B.α内不存在与l平行的直线C.α内存在唯一的直线与l平行D.α内的直线与l都相交【解析】由题意知,直线l与平面α相交,则直线l与平面α内的直线只有相交和异面两种位置关系,因而只有选项B是正确的.【答案】B4.(2012·四川高考)如图7-3-1,在正方体ABCD-A1B1C1D1中,M、N分别是棱CD、CC1的中点,则异面直线A1M与DN所成的角的大小是________.【解析】如图,取CN的中点K,连接MK,则MK为△CDN的中位线,所以MKDN.∥所以∠A1MK为异面直线A1M与DN所成的角.连接A1C1,AM.设正方体棱长为4,【答案】90°则A1K=(42)2+32=41,MK=12DN=1242+22=5,A1M=42+42+22=6,∴A1M2+MK2=A1K2,∴∠A1MK=90°.如图7-3-2所示,四边形ABEF和ABCD都是梯形,BC綊12AD,BE綊12FA,G、H分别为FA、FD的中点.(1)证明:四边形BCHG是平行四边形;(2)C、D、F、E四点是否共面?为什么?【思路点拨】(1)利用中位线的性质证明GH綊BC即可.(2)法一证明D点在EF、CH确定的平面内.法二延长FE、DC分别与AB交于M,M′,可证M与M′重合,从而FE与DC相交证得四点共面.【尝试解答】(1)由已知FG=GA,FH=HD,得GH綊12AD.又BC綊12AD,∴GH綊BC,∴四边形BCHG是平行四边形.(2)法一由BE綊12AF,且G为FA中点知BE綊GF,∴四边形BEFG为平行四边形,∴EF∥BG.由(1)知BG∥CH,∴EF∥CH,∴EF与CH共面.又D∈FH,∴C、D、F、E四点共面.法二如图所示,延长FE,DC分别与AB交于点M,M′, BE綊12AF,∴B为MA中点, BC綊12AD,∴B为M′A中点,∴M与M′重合,即FE与DC交于点M(M′),∴C、D、F、E四点共面.已知:空间四边形ABCD(如图7-3-3所示),E、F分别是AB、AD的中点,G、H分别是BC、CD上的点,且CG=13BC,CH=13DC.求证:(1)E、F、G、H四点共面;(2)三直线FH、EG、AC共点.【证明】(1)连接EF、GH, E、F分别是AB、AD的中点,∴EF∥BD.又 CG=13BC,CH=13DC,∴GH∥BD,∴EF∥GH,∴E、F、G、H四点共面.(2)易知FH与直线AC不平行,但共面,∴设FH∩AC=M,∴M∈平面EFHG,M∈平面ABC.又 平面EFHG∩平面ABC=EG,∴M∈EG,∴FH、EG、AC共点.(1)如图7-3-4,在正方体ABCD—A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列判断错误的是()A.MN与CC1垂直B.MN与AC垂直C.MN与BD平行D.MN与A1B1平行空间两...