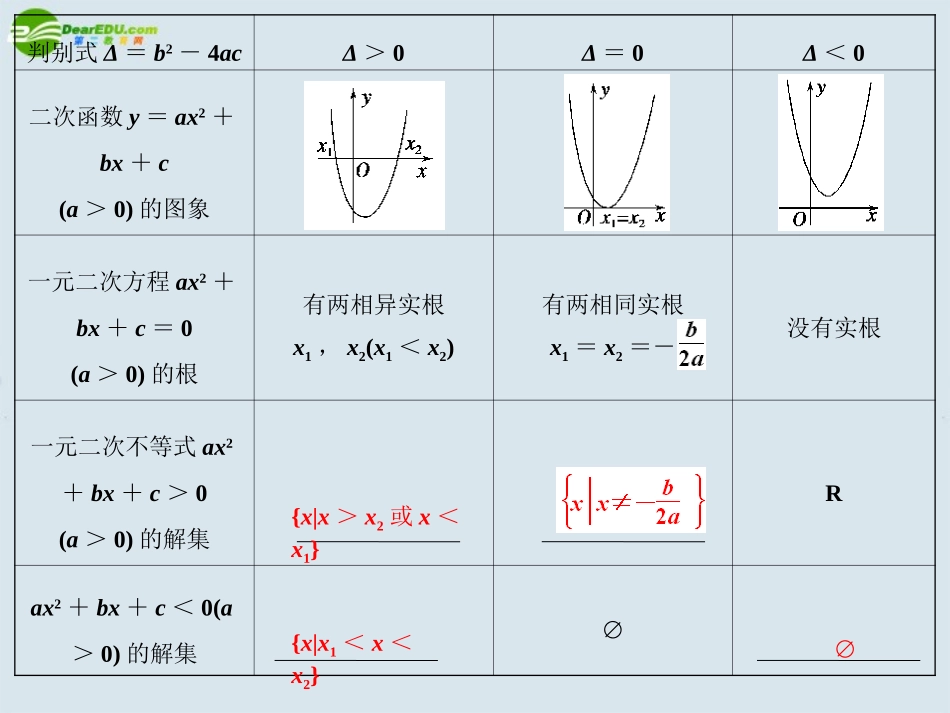
【考纲下载】1.会从实际情境中抽象出一元二次不等式模型.2.通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系.3.会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图.第2讲一元二次不等式一元二次不等式与相应二次函数、方程的关系(填表)判别式Δ=b2-4acΔ>0Δ=0Δ<0二次函数y=ax2+bx+c(a>0)的图象一元二次方程ax2+bx+c=0(a>0)的根有两相异实根x1,x2(x1<x2)有两相同实根x1=x2=-没有实根一元二次不等式ax2+bx+c>0(a>0)的解集Rax2+bx+c<0(a>0)的解集∅{x|x>x2或x<x1}{x|x1<x<x2}∅1.已知集合A={x|x2-7x+6≤0,x∈Z},B={x|2x2-x-6>0,x∈Z},则A∩B的子集个数为()A.16B.32C.15D.8解析:由x2-7x+6≤0,得1≤x≤6,∴A={1,2,3,4,5,6},由2x2-x-6>0,得x<-或x>2,∴B={x|x<-或x>2,且x∈Z},∴A∩B={3,4,5,6},∴A∩B的子集共有24=16个.答案:A2.已知不等式x2+ax+4<0的解集为空集,则a的取值范围是()A.-4≤a≤4B.-4<a<4C.a≤-4或a≥4D.a<-4或a>4解析:Δ=a2-16≤0,∴-4≤a≤4.答案:A3.不等式≥2的解集是()A.B.C.∪(1,3]D.∪(1,3]解析:解法一:首先x≠1,在这个条件下根据不等式的性质原不等式可以化为x+5≥2(x-1)2,即2x2-5x-3≤0,即(2x+1)(x-3)≤0,解得-≤x≤3,故原不等式的解集是∪(1,3].解法二:特殊值检验法.首先x≠1,排除B,显然x=0,x=2是不等式的解,排除A、C.答案:D4.已知(ax-1)(x-1)>0的解集是{x|x<1或x>2},则实数a的值为________.解析:由不等式解集是{x|x<1或x>2}可知=2,∴a=答案:解含参数的一元二次不等式可按如下步骤进行:1.二次项若含有参数应讨论是等于0、小于0、还是大于0.然后将不等式转化为二次项系数为正的形式.2.判断方程的根的个数,讨论判别式Δ与0的关系.3.确定无根时可直接写出解集,确定方程有两个根时,要讨论两根的大小关系,从而确定解集的形式.【例1】解不等式:ax2-(a+1)x+1<0.思维点拨:先考虑a=0,再考虑a≠0,然后因式分解,比较根的大小,得出解集.解:若a=0,原不等式⇔-x+1<0⇔x>1.若a<0,原不等式⇔(x-1)>0⇔x<或x>1.若a>0,原不等式⇔(x-1)<0(*).当a=0时,解集为{x|x>1};当0
1时,解集为其解的情况应由与1的大小关系决定,故①当a=1时,(*)式⇔x∈∅;②当a>1时,(*)式⇔0变形为(x-a)(x-a2)>0.当a<0时,有aa2};当0a2,解集为{x|xa};当a>1时,有aa2};当a=0时,解集为{x|x∈R,且x≠0};当a=1时,解集为{x|x∈R,且x≠1}.三个“二次”各自内涵丰富,而又联系密切,相互渗透.在解相关问题时,要灵活进行转化,并要重视函数与方程、数形结合等数学思想方法的综合运用.【例2】已知不等式ax2+bx+c>0(a≠0)的解集为{x|α0可化为x2+<0.方程x2+=0的两个根为α、β.∴=-(α+β),=αβ. 0<α<β,a<0,∴>0,即c<0.因而不等式cx2+bx+a<0可化为x2+>0,可得是方程x2+=0的两个根.又 0<α<β,∴故不等式cx2+bx+a<0的解集为函数式中含有两个参数,知道其中一个的范围求另一个的取值范围,常用的方法有:1.ax2+bx+c>0恒成立的充要条件是ax2+bx+c<0恒成立的充要条件是2.分离参数法,即化为a>f(x)恒成立或af(x)恒成立⇔a>f(x)max;a0在x∈[0,1]上恒成立,求实数a的取值范围.思维点拨:令f(x)=x2+ax-a+1,则f(x)>0在x∈[0,1]上恒成立,等价于二次函数f(x)在[0,1]上的最小值大于零或分式函数(分离参数)在给定...