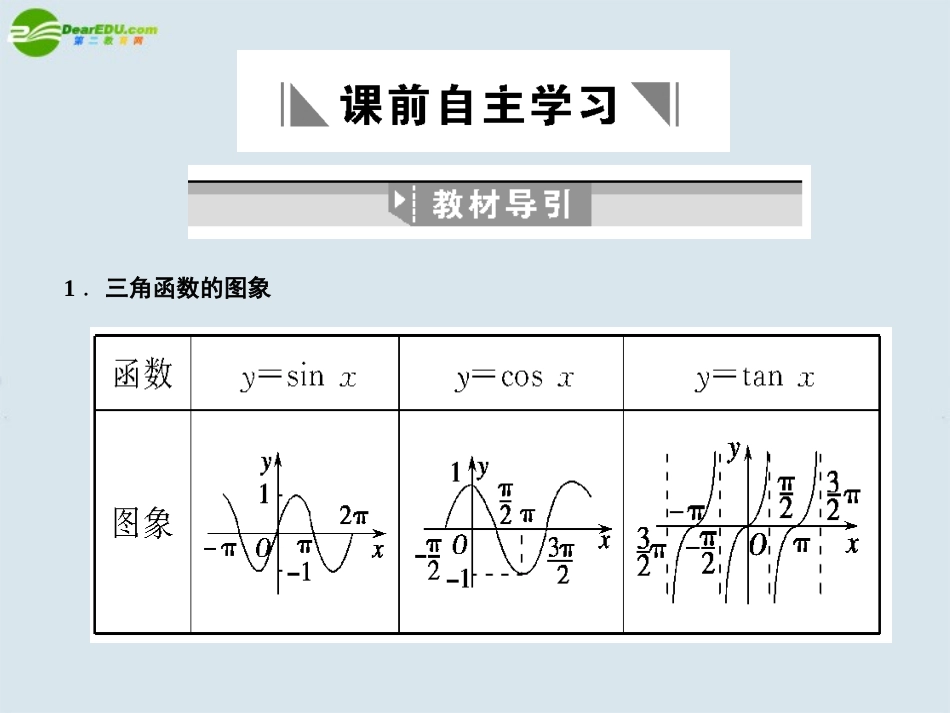
【考纲下载】1.能画出y=sinx,y=cosx,y=tanx的图象.2.了解函数y=Asin(ωx+φ)的物理意义;能画出y=Asin(ωx+φ)的图象,了解参数A,ω,φ对函数图象变化的影响.第3讲三角函数的图象1.三角函数的图象五点画图法(1)y=sinx,x∈[0,2π]上的五个关键点为:,,,,.(2)y=cosx,x∈[0,2π]上的五个关键点为:,,,,.(0,0)(π,0)(2π,0)(0,1)(π,-1)(2π,1)2.【思考】用“五点法”作y=Asin(ωx+φ)(A>0,ω>0)的具体做法?答案:设X=ωx+φ,由X取0,,π,,2π来求相应的x值,及对应的y值,再描点作图.图象变换函数y=Asin(ωx+φ)(A>0,ω>0)的图象可由函数y=sinx的图象作如下变换得到:把y=sinx图象上所有的点向(φ>0)或向(φ<0)平行移动个单位.左|φ|把y=sin(x+φ)图象上各点的横坐标(0<ω<1)或(ω>1)到原来的倍(纵坐标不变).伸长缩短右3.把y=sin(ωx+φ)图象上各点的纵坐标(A>1)或(0
0,ω>0)在闭区间[-π,0]上的图象如图所示,则ω=________.解析:观察函数图象可得周期,又由函数y=Asin(ωx+φ)得答案:34.常用三角函数的图象和性质(奇偶性、定义域、值域、单调性)来判断函数的图象,高考中这一题型常以选择题的形式出现,此时亦可用排除法.(2009·浙江卷)已知a是实数,则函数f(x)=1+asinax的图象不可能是()【例1】思维点拨:对实数a分a=0,01三种情况验证.解析:当a=0时,f(x)=1,图象即为C项;当02π,图象即为A项;当a>1时,三角函数的周期为T=<2π,图象即为B项.答案:D五点作图法的一般步骤是:1.将函数整理成y=Asin(ωx+φ)的形式;2.列表,令z=ωx+φ,分别令z=0,,π,,2π,求出相应的x值x1,x2,x3,x4,x5,及相应的y值0,A,0,-A,0,列成表格;3.描点,在坐标系中作出五个点(x1,0),(x2,A),(x3,0),(x4,-A),(x5,0),即函数y=Asin(ωx+φ)的图象的一个周期上的五个点;4.连线,用平滑曲线连接起五个点,再向两端延伸即可得到函数在整个定义域上的图象.已知函数f(x)=2sinx·(sinx+cosx),(1)求f(x)的最小正周期;(2)画出函数y=f(x)在区间上的图象.思维点拨:按以上步骤进行.解:(1)f(x)=2sin2x+2sinxcosx=1-cos2x+sin2x=∴f(x)的最小正周期为π.【例2】故函数y=f(x)在区间上的图象如下:(2)由(1)知设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线x=,画出函数y=f(x)在区间[0,π]上的图象.解: x=是函数y=f(x)的图象的对称轴,变式2:故函数y=f(x)在区间[0,π]上的图象是在三角函数图象的平移问题中首先要搞清楚是哪个函数图象变换到哪个函数图象,分析清楚自变量变化的过程.【例3】(2009·安徽合肥)已知函数指出的图象经过怎样的平移变换后得到的图象关于坐标原点对称.到的图象关于坐标原点对称.拓展3:本例条件不变,指出y=f(x)的图象经过怎样的平移变换后得到的图象关于y轴对称.函数y=Asin(ωx+φ)(ω>0)解析式的确定,也就是参数A,ω,φ的确定,通常方法为:1.A可由图象的最高(低)点确定;2.ω一般通过周期公式T=来求解,因而要求出ω,关键在于求出周期.一般地,函数的周期可以由最高点、最低点、零点的坐标或者对称轴的方程、对称中心的坐标等来求解;3.φ可用代入法求解,即把图象上的一个已知点代...