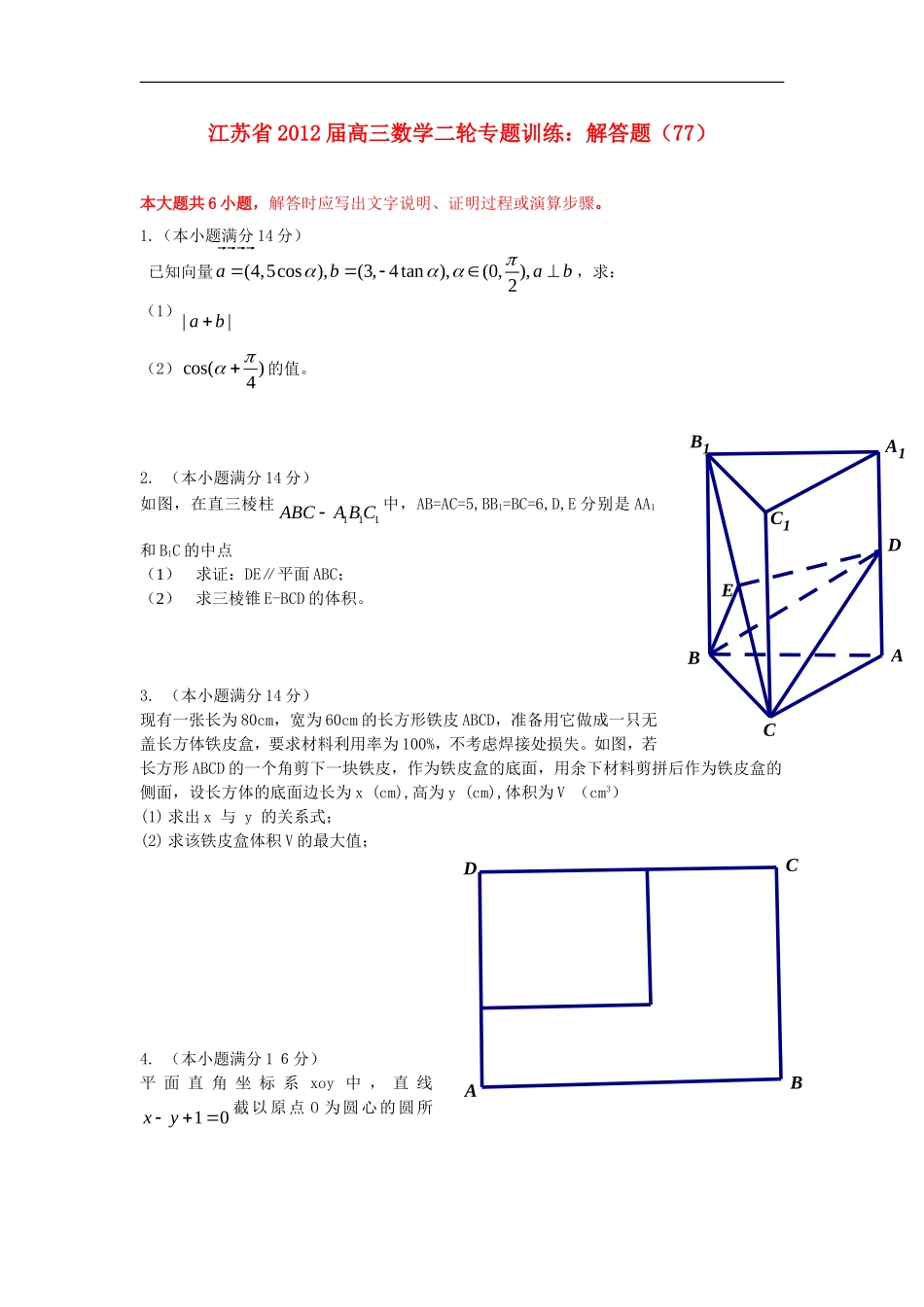
江苏省2012届高三数学二轮专题训练:解答题(77)本大题共6小题,解答时应写出文字说明、证明过程或演算步骤。1.(本小题满分14分)已知向量(4,5cos),(3,4tan),(0,),2abab,求:(1)||ab(2)cos()4的值。2.(本小题满分14分)如图,在直三棱柱111ABCABC中,AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点(1)求证:DE∥平面ABC;(2)求三棱锥E-BCD的体积。3.(本小题满分14分)现有一张长为80cm,宽为60cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失。如图,若长方形ABCD的一个角剪下一块铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面边长为x(cm),高为y(cm),体积为V(cm3)(1)求出x与y的关系式;(2)求该铁皮盒体积V的最大值;4.(本小题满分16分)平面直角坐标系xoy中,直线10xy截以原点O为圆心的圆所EDB1C1A1CBADCBA得的弦长为6(1)求圆O的方程;(2)若直线l与圆O切于第一象限,且与坐标轴交于D,E,当DE长最小时,求直线l的方程;(3)设M,P是圆O上任意两点,点M关于x轴的对称点为N,若直线MP、NP分别交于x轴于点(m,0)和(n,0),问mn是否为定值?若是,请求出该定值;若不是,请说明理由。5.(本小题满分16分)已知函数2()()xfxaxxe,其中e是自然数的底数,aR。(1)当0a时,解不等式()0fx;(2)若()fx在[-1,1]上是单调增函数,求a的取值范围;(3)当0a时,求整数k的所有值,使方程()2fxx在[k,k+1]上有解。6.(本小题满分16分)设数列{}na的前n项和为nS,已知1(,nnSpSqpq为常数,*nN),eg1232,1,3aaaqp(1)求p,q的值;(2)求数列{}na的通项公式;(3)是否存在正整数m,n,使1221mnmnSmSm成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。1.⑴因为ab,所以435cos4tan0,………………………2分解得3sin5,又因为π(0,)2,………………………………………4分所以4cos5,sin3tancos4,………………………………………6分所以(7,1)ab=,因此22||7152ab.………………………8分⑵πππcoscoscossinsin444…………………………………12分42322525210.…………………………………………………14分2.⑴取BC中点G,连接AG,EG,因为E是1BC的中点,所以EG∥1BB,且112EGBB.ABC1A1B1CDEG(第16题)由直棱柱知,11AABB∥,而D是1AA的中点,所以EGAD∥,…………………………4分所以四边形EGAD是平行四边形,所以EDAG∥,又DE平面ABC,AGABC平面所以DE∥平面ABC.………………………7分⑵因为1ADBB∥,所以AD∥平面BCE,所以EBCDDBCEABCEEABCVVVV,………………………………………10分由⑴知,DE∥平面ABC,所以11136412326EABCDABCVVADBCAG.…………………14分3.⑴由题意得244800xxy,即248004xyx,060x.……………………………………………6分⑵铁皮盒体积222348001()120044xVxxyxxxx,………………10分/23()12004Vxx,令/()0Vx,得40x,……………………………12分因为(0,40)x,/()0Vx,()Vx是增函数;(40,60)x,()0Vx,()Vx是减函数,所以31()12004Vxxx,在40x时取得极大值,也是最大值,其值为332000cm.答:该铁皮盒体积V的最大值是332000cm.……………………14分4.⑴因为O点到直线10xy的距离为12,………………………2分所以圆O的半径为2216()()222,故圆O的方程为222xy.………………4分⑵设直线l的方程为1(0,0)xyabab,即0bxayab,由直线l与圆O相切,得222abab,即221112ab,……………6分2222222112()()8DEababab≥,当且仅当2ab时取等号,此时直线l的方程为20xy.………10分⑶设11(,)Mxy,22(,)Pxy,则11(,)Nx...