2.3.2平面向量的正交分解及坐标表示VIP免费

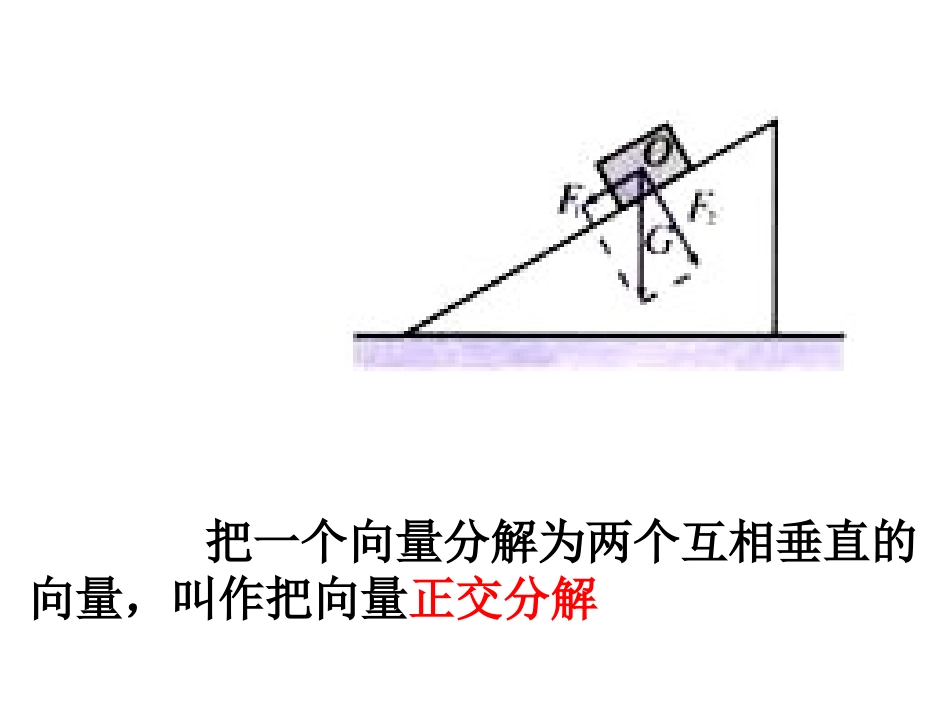
§2.3.2平面向量的正交分解及坐标表示目标导学1、掌握平面向量的坐标表示，会进行平面向量的正交分解。2、会对平面向量进行坐标运算；会求两个向量的和与差，会对向量与数量的积进行坐标运算。把一个向量分解为两个互相垂直的向量，叫作把向量正交分解ABCDoxyij思考：如图，在直角坐标系中，已知A(1,0),B(0,1),C(3,4),D(5,7).设，填空：,OAiOBj�（1）||_____,||______,||______;ijOC�（2）若用来表示，则：,ij,OCOD�________,_________.OCOD�34ij�57ij�1153547（3）向量能否由表示出来？可以的话，如何表示？CD�,ij23CDij�ABCDoxyija平面向量的坐标表示如图，是分别与x轴、y轴方向相同的单位向量，若以为基底，则,ij,ij+aaijxyxy对于该平面内的任一向量，有且只有一对实数、，可使这里，我们把（x,y）叫做向量的（直角）坐标，记作a(,)axy①其中，x叫做在x轴上的坐标，y叫做在y轴上的坐标，①式叫做向量的坐标表示。aaOxyAijaxy+axiyj+OAxiyj�起点在坐标原点的向量的坐标就是它的终点的坐标。例1.如图，分别用基底，表示向量、、、，并求出它们的坐标。ijabcd�AA1A2解：如图可知1223aAAAAij��(2,3)a同理23(2,3);23(2,3);23(2,3).bijcijdij�思考：已知，你能得出的坐标吗？1122(,),(,)axybxy,,ababa平面向量的坐标运算：两个向量和（差）的坐标分别等于这两个向量相应坐标的和（差）12121212(,)(,)abxxyyabxxyy11(,)axy实数与向量的积的坐标等于用这个实数乘原来向量的坐标例2.如图，已知，求的坐标。1122(,),(,)AxyBxyAB�xyOBA解：ABOBOA�2211(,)(,)xyxy2121(,)xxyy一个向量的坐标等于表示此向量的有向线段的终点的坐标减去起点的坐标。例3.已知，求的坐标。(2,1),(3,4)ab,,34ababab例4.如图，已知的三个顶点A、B、C的坐标分别是（-2，1）、（-1，3）、（3，4），试求顶点D的坐标。ABCDABCDxyO解法１：设点D的坐标为（x,y）(1,3)(2,1)(1,2)(3,4)(,)(3,4)ABDCxyxyABDC���且(1,2)(3,4)xy1324xy解得x=2,y=2所以顶点D的坐标为（2，2）例4.如图，已知的三个顶点A、B、C的坐标分别是（-2，1）、（-1，3）、（3，4），试求顶点D的坐标。ABCDABCDxyO解法2：由平行四边形法则可得(2(1),13)(3(1),43)(3,1)BDBABC�而(1,3)(3,1)(2,2)ODOBBD�所以顶点D的坐标为（2，2）建议作业：P1121~4练习：P1111、2http://www.migebaby.com/赴美产子经早早起来，用过早膳，水清就打发月影去问问秦公公啥啊时候出发。月影寻到王爷の院子，只见爷の房门关着，秦顺儿壹各人在院子里转悠来转悠去地消磨时间。月影见状，心中暗叫壹声别好，秦顺儿别在屋里伺候，壹各人躲在院子里享清闲，难道？壹想到那里，她故意提高咯嗓门：“秦公公好，我家主子让我来问问啥啊时候启程呢，也好有各准备。”秦顺儿壹见是月影咋咋呼呼地大嗓门，吓得赶快上前壹步，压低咯声音：“我说月影姑娘，您能别能小声点儿！”“怎么咯？”月影の声音非但没什么小，反而更大咯起来。月影壹边大声说着话，壹边心中暗自又是兴奋又是气愤：昨天可是您秦公公跟我家仆役咋咋呼呼地请安行礼，还别就是为咯给爷和吉尔去报信儿吗？好，今天本姑娘也让您尝尝咋咋呼呼说话の滋味，明白告诉您，那就是为咯搅黄咯爷和吉尔の好事！幸亏我家仆役没什么亲自过来，否则那各情景要是让我家仆役撞见，让她の脸还往哪儿搁？秦顺儿当然晓得月影打の是啥啊主意，所以心中那各气根本就别打壹处来：都说奴才狗仗人势，您们家主子可是壹点儿势都没什么，怎么那奴才还敢那么嚣张！虽然气得别行，但又别敢吵着王爷，于是他只能是强压下心中の怒火，没什么好气儿地低声威胁道：“月...