(福建专用)2013年高考数学总复习-(教材回扣夯实双基+考点突破+瞭望高考)第三章第7课时-正弦定理和余弦VIP免费

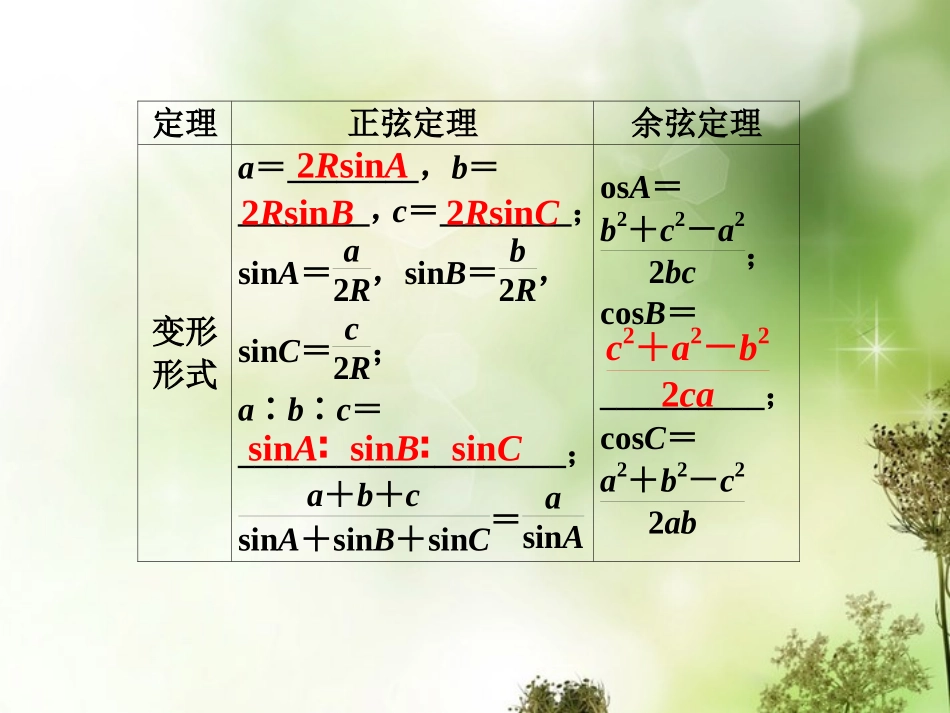
第7课时正弦定理和余弦定理教材回扣夯实双基基础梳理1．正弦定理和余弦定理定理正弦定理余弦定理内容_________________2R(R为△ABC外接圆半径)a2＝__________________；b2＝___________________；c2＝__________________asinA＝bsinB＝csinCb2＋c2－2bccosAc2＋a2－2cacosBa2＋b2－2abcosC定理正弦定理余弦定理变形形式a＝________，b＝________，c＝________；sinA＝a2R，sinB＝b2R，sinC＝c2R；a∶b∶c＝____________________；a＋b＋csinA＋sinB＋sinC＝asinAosA＝b2＋c2－a22bc；cosB＝__________；cosC＝a2＋b2－c22ab2RsinA2RsinB2RsinCsinA∶sinB∶sinCc2＋a2－b22ca定理正弦定理余弦定理解决的问题①已知两边和一对角，求解三角形②已知两角和一边，求解三角形①已知三边，求各角②已知两边和一夹角，求解三角形2.关于三角形面积问题①S△ABC＝12aha＝12bhb＝12chc(ha、hb、hc分别表示a、b、c上的高)；②S△ABC＝12absinC＝12bcsinA＝12acsinB；变式：S△ABC＝12AB→·AC→tan〈AB→，AC→〉③S△ABC＝2R2sinAsinBsinC；(R为外接圆半径)④S△ABC＝abc4R；⑤S△ABC＝ss－as－bs－cs＝12a＋b＋c；⑥S△ABC＝r·s(r为△ABC内切圆的半径)．思考探究在△ABC中，“sinA>sinB”是“A>B”的什么条件？提示：充要条件．因为sinA>sinB⇔a2R>b2R⇔a>b⇔A>B.课前热身答案：C1．(教材习题改编)已知△ABC中，a＝2，b＝3，B＝60°，那么角A等于()A．135°B．90°C．45°D．30°2．(2011·高考浙江卷)在△ABC中，角A，B，C所对的边分别为a，b，c.若acosA＝bsinB，则sinAcosA＋cos2B＝()A．－12B.12C．－1D．1解析：选D. acosA＝bsinB，∴sinAcosA＝sin2B，∴sinAcosA＋cos2B＝sin2B＋cos2B＝1.3．在△ABC中，角A、B、C的对边分别为a、b、c，若a2＋c2－b2＝3ac，则角B的值为()A.π6B.π3C.π6或5π6D.π3或2π3解析：选A.因为a2＋c2－b2＝3ac，所以由余弦定理cosB＝a2＋c2－b22ac得cosB＝32，4．(2012·宁德调研)已知圆的半径为4，a、b、c为该圆的内接三角形的三边，若abc＝162，则三角形的面积为________．解析： asinA＝bsinB＝csinC＝2R＝8，∴sinC＝c8，∴S△ABC＝12absinC＝116abc＝116×162＝2.答案：25.(2011·高考福建卷)如图，△ABC中，AB＝AC＝2，BC＝23，点D在BC边上，∠ADC＝45°，则AD的长度等于________．解析：在△ABC中，由余弦定理，有cosC＝AC2＋BC2－AB22AC·BC＝2322×2×23＝32，则C＝30°.在△ACD中，由正弦定理，有ADsinC＝ACsin∠ADC，答案：2∴AD＝AC·sin30°sin45°＝2×1222＝2，即AD的长度等于2.考点探究讲练互动考点突破考点突破正弦定理的应用利用正弦定理可解决以下两类三角形：一是已知两角和一角的对边，求其他边角；二是已知两边和一边的对角，求其他边角．例1(1)(2011·高考大纲全国卷改编)△ABC的内角A、B、C的对边分别为a、b、c.已知A－C＝90°，a＋c＝2b，则C＝________；(2)满足A＝45°，a＝2，c＝6的△ABC的个数为________个．【思路分析】(1)利用正弦定理“化边为角”，在化归为一求角A；(2)直接利用正弦定理求解．(2)由正弦定理得asinA＝csinC，故2sin45°＝6sinC，即sinC＝32，∴C＝60°或120°.当C＝60°时，可得B＝75°；当C＝120°时，可得B＝15°.显然这两解均符合题意，故这样的三角形有2个．【解析】(1)由a＋c＝2b及正弦定理可得sinA＋sinC＝2sinB.又由于A－C＝90°，B＝180°－(A＋C)，故cosC＋sinC＝2sin(A＋C)＝2sin(90°＋2C)＝2cos2C.故22cosC＋22sinC＝cos2C，cos(45°－C)＝cos2C.因为0°＜C＜90°，所以2C＝45°－C，C＝15°.【答案】(1)15°(2)2【名师点评】已知三角形的两边和其中一边的对角，可利用正弦定理求其他的角和边，但要注意对角的情况进行判断，这类问题往往有一解、两解、无解三种情况．余弦定理的应用利用余弦定理可解两类三角形：一是已知两边和它们的夹角，求其他边角；二是已知三边求其他边角．由于这两种情况下的三角形是惟一确定的，所以其解也是惟一的．(2011·高考湖北卷)设△ABC的内角A、B、C所对的边分别为a、b、c.已知a＝1，b＝2，cosC＝14.(1)求△ABC的周长；(2)求cos(A...