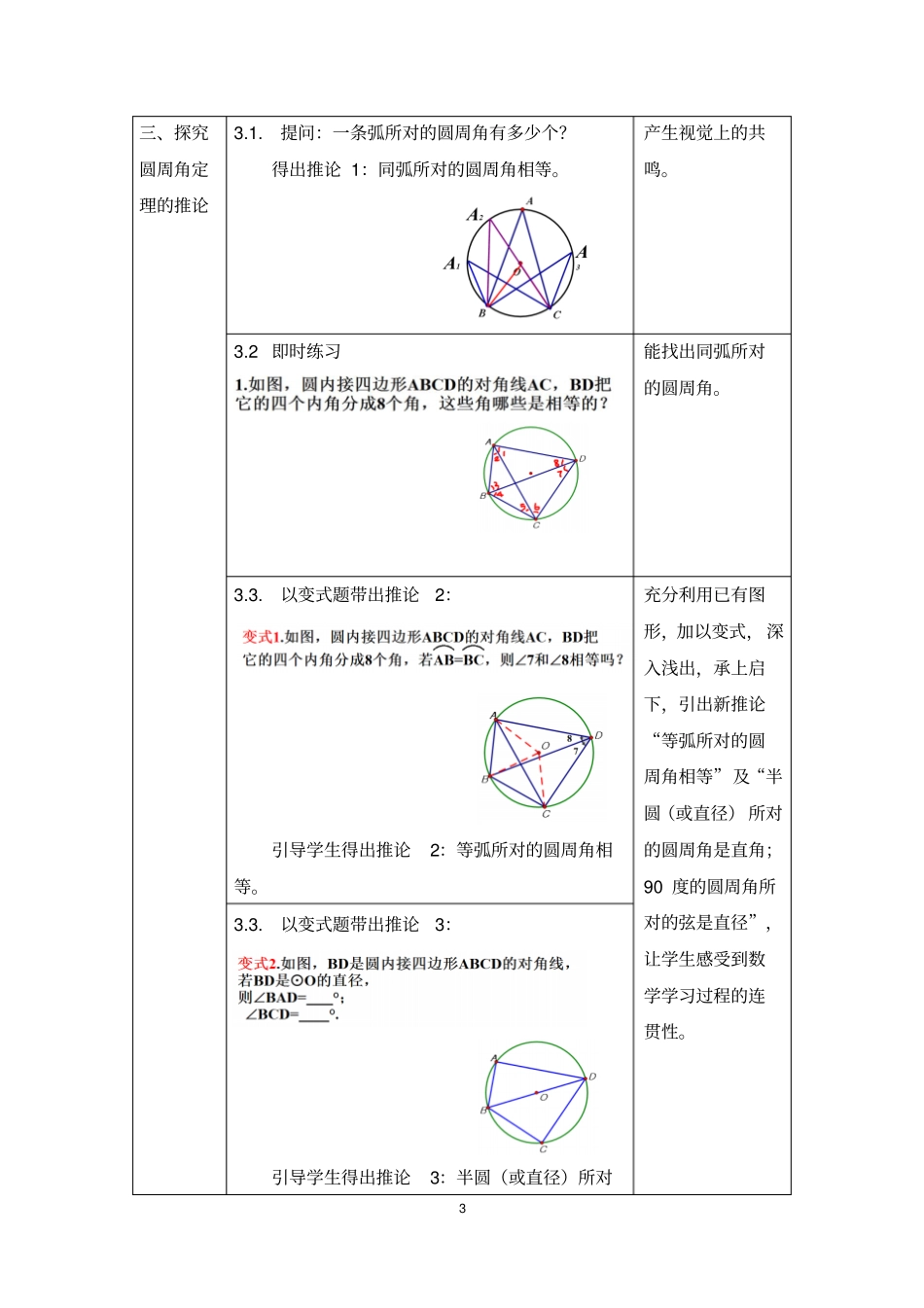
1《圆周角》微课程设计学情分析:学生已经认识圆的弦、弧、圆心角,知道圆心角定理,并能简单说理。教学目标:1.能判断圆周角,会用符号语言和文字语言叙述圆周角定理;2.通过完全归纳法探究圆周角定理,能推理验证“圆周角与圆心角的关系”;3.能用圆周角定理解决简单的几何问题,能进行简单的口头说理,并产生解决问题的成就感。课程工具:CamtasiaStudio录屏软件,几何画板,PowerPoint特色介绍:1.由已学的圆心角类比法导出圆周角的概念,并借助“洋葱数学”有趣导入新知识,引起学生的注意;2.渗透完全归纳法,采用几何法和代数法证明圆周角定理,让学生体验数形结合的强大功能;3.通过微调图形、变式练习逐步推导圆周角定理的推论,让学生感受数学学习的连贯性;4.课后补充练习分不同难度系数,观看微课程的学生可根据自身学习能力选择习题,使本微课程更具有实用性;5.本微课程“此起彼伏”,使不同层次的学生通过本微课程的学习在数学思维上都能有所提升。教学重点:完全归纳法探究圆周角定理。教学难点:探究圆周角定理时如何分情况讨论。教学过程:教学环节过程与问题设计意图2一、圆周角的概念1.1.回顾:什么叫圆心角?指出图中的圆心角?以旧带新,渗透类比学习法。1.2.类比法给出圆周角的定义:顶点在圆上,并且两边都与圆相交的角。1.3.即时练习:下列各图中的∠BAC是否为圆周角?巩固对圆周角概念的理解。二、探究圆周角定理2.1.猜想:如图,连接BO,CO,得圆心角∠BOC。试猜想∠BAC与∠BOC存在怎样的数量关系。让学生动手,结合思考,对自己的猜想产生较为深刻的印象。2.2.为什么要分情况讨论?怎么分情况讨论?思考:还可能有其他情况吗?渗透完全归纳法,体验思考过程,提高个人的符号语言表达能力。2.3.得出圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。以文字陈述,进一步理解并发自内心接受圆周角定理。3三、探究圆周角定理的推论3.1.提问:一条弧所对的圆周角有多少个?得出推论1:同弧所对的圆周角相等。产生视觉上的共鸣。3.2即时练习能找出同弧所对的圆周角。3.3.以变式题带出推论2:引导学生得出推论2:等弧所对的圆周角相等。充分利用已有图形,加以变式,深入浅出,承上启下,引出新推论“等弧所对的圆周角相等”及“半圆(或直径)所对的圆周角是直角;90度的圆周角所对的弦是直径”,让学生感受到数学学习过程的连贯性。3.3.以变式题带出推论3:引导学生得出推论3:半圆(或直径)所对4的圆周角是直角;90度的圆周角所对的弦是直径。四、即时练习4.1.变式(备注:能口头说理即可,不要求书写过程)两个问题分层次设计,从易到难,加强对圆周角定理及其推论的理解。4.2习题小结:及时总结解题的经验和方法。五、课堂小结以图形帮助学生回忆圆周角定理及推论:让学生在大脑里形成图形记忆法,将整节课内容串联成一条完整的线。六、补充练习6.1.(难度系数3)1.如图,AD为⊙O的直径,∠ABC=75°,且AC=BC,则∠BED=__________.分层布置作业,学生根据自己的情况选择题目难度系数,尽量使每个学生都能有所收获.6.2.(难度系数4)2.已知:如图,AB是圆O的直径,AB=AC,∠BAC=45°。(1)求∠EBC的度数;(2)求证:5BD=CD。