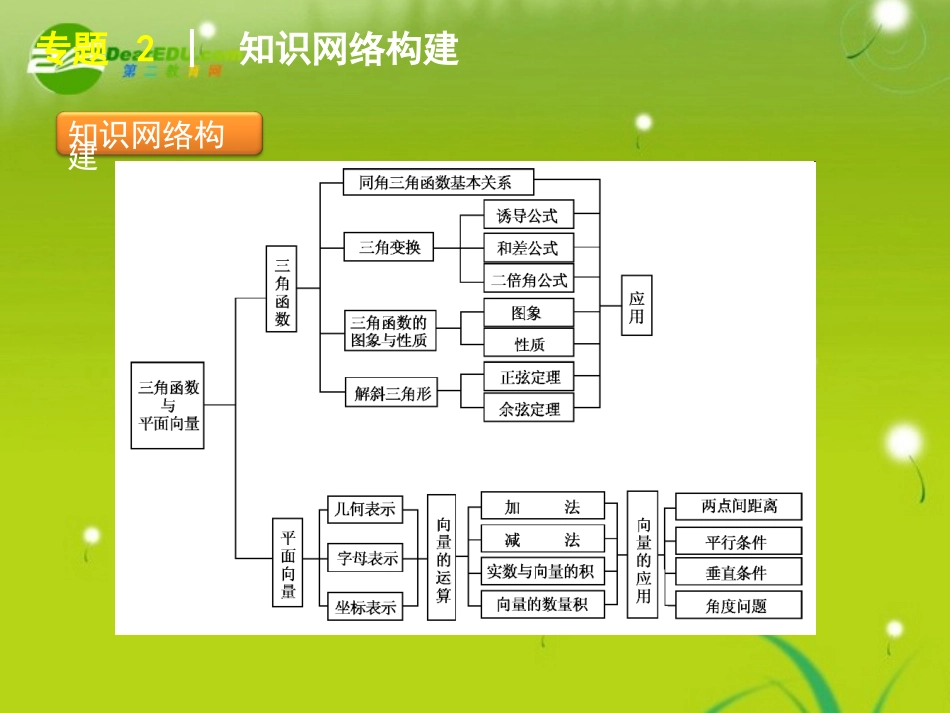
专题2三角函数与平面向量知识网络构建专题2│知识网络构建考情分析预测专题2│考情分析预测1.三年高考回顾年份内容题号与分值2008三角函数性质向量运算三角函数综合三角函数实际应用第1题5分;第5题5分;第15题14分;第17题14分.专题2│考情分析预测年份内容题号与分值2009向量运算三角函数图象三角函数与向量综合第2题5分;第4题5分;第15题14分.2010三角函数图象正余弦定理与三角变换向量综合解三角形第10题5分;第13题5分;第15题14分;第17题14分.专题2│考情分析预测2.命题特点探究江苏近三年高考三角函数与平面向量的试题,一般是两到三个小题和一个大题;解答题一般都为基础题,处在送分题的位置;而在两个到三个小题中,08年和09年有一个较容易,而另一个为中档题,2010年15,17题出了两个有关三角函数和向量的解答题,且位置靠前,所以填空题的难度相对加大,但整体得分与往年相比没有大的变化.从近三年高考命题来看,平面向量的数量积,正余弦定理的运用,三角函数的图象和性质,尤其是三角函数的周期、最值、单调性、图象变换、特征分析(对称轴、对称中心)和三角函数式的恒等变形等仍是命题热点.专题2│考情分析预测3.命题趋势预测预计2011年高考本专题的命题方向是:①考小题,重在基础:有关三角函数的小题,其考查的重点在于基础知识:解析式、图象及图象变换、两域(定义域、值域)、四性(单调性、奇偶性、对称性、周期性)以及简单的三角变换(求值、化简及比较大小).有关平面向量的小题,其考查重点仍会是数量积及相关运算.②考大题,重在本质:有关三角函数和平面向量的大题即解答题,通过公式变形、转换来考查思维能力的题目已经没有了,而是考查基础知识、基本技能和基本方法.专题2│考情分析预测③考应用,融入三角形之中:这种题型既能考查解三角形的知识与方法,又能考查运用三角公式进行恒等变换的技能,故近年来倍受命题者的青睐.主要解法是充分利用三角形的内角和定理、正(余)弦定理、面积公式等,并结合三角公式进行三角变换,从而获解.④考综合,体现三角向量的工具和传接作用:由于近年高考命题突出以能力立意,加强对知识综合性和应用性的考查,故常常在知识的交汇点处命题.因而对三角向量有时会综合在一起来考查.但与其他知识交汇的可能性不大.第第33讲三角函数的图象与性质讲三角函数的图象与性质第3讲│三角函数的图象与性质主干知识整合第3讲│主干知识整合对于函数y=Asin(ωx+φ)要关注下面几个问题:①定义域:R.②值域:-A,A.当x=2kπ+π2-φω(k∈Z)时,y取最大值A;当x=2kπ-π2-φω(k∈Z)时,y取最小值-A.③周期性:周期函数,周期为2πω.第3讲│主干知识整合④单调性:单调递增区间是2kπ-π2-φω,2kπ+π2-φω(k∈Z);单调递减区间是2kπ+π2-φω,2kπ+3π2-φω(k∈Z).⑤对称性:函数图象与x轴的交点是对称中心,即对称中心是kπ-φω,0,k∈Z,对称轴与函数图象的交点的纵坐标是函数的最值,即对称轴是直线x=kπ+π2-φω,其中k∈Z.第3讲│主干知识整合⑥函数y=Asin(ωx+φ)(A>0,ω>0)中,A影响函数图象的最高点和最低点,即函数的最值;ω影响函数图象每隔多少重复出现,即函数的周期;φ影响函数的初相.⑦对于函数y=Asin(ωx+φ)(A>0,ω>0)的图象,相邻的两个对称中心或两条对称轴相距半个周期;相邻的一个对称中心和一条对称轴相距四分之一个周期.要点热点探究第3讲│要点热点探究例1若函数f(x)=Asin(ωx+φ)ω>0,A>0,|φ|<π2的图象如图2-3-1所示,这个函数的解析式为________.图2-3-1►探究点一三角函数的图象变换与解析式第3讲│要点热点探究f(x)=3sin2x+π3【解析】由题意知:周期T=25π6-π3=π,∴ω=2πT=2.则f(x)=Asin(2x+φ),则π3,0为五点作图中的第三点,所以2×π3+φ=π,即φ=π3,则f(x)=Asin2x+π3,因为点0,32在原函数的图象上,故Asinπ3=32,所以A=3,综上知f(x)=3sin2x+...