相似三角形的性质1VIP免费

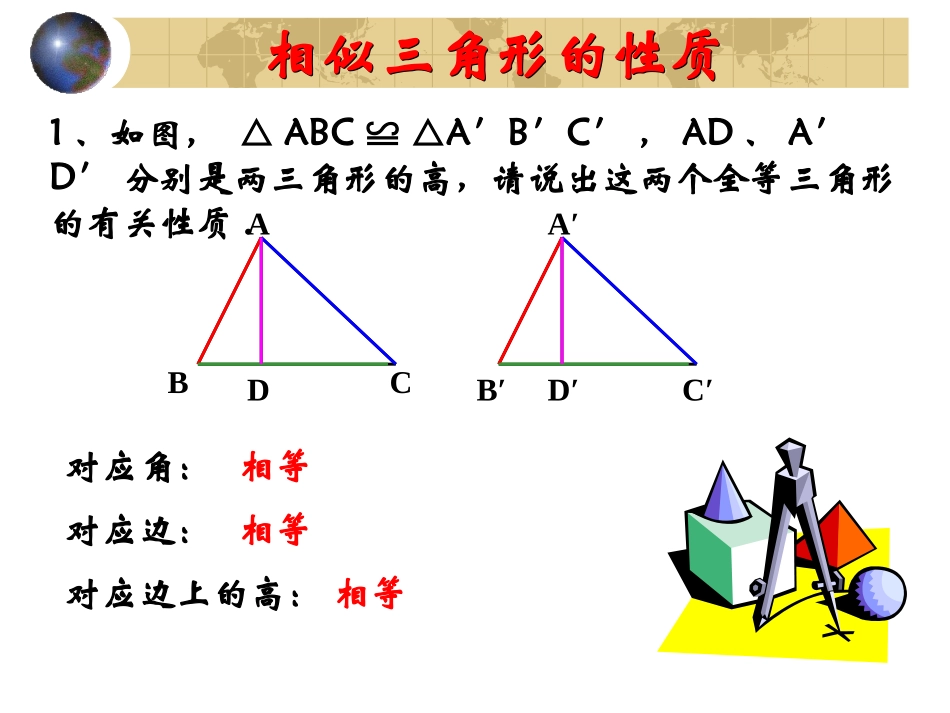
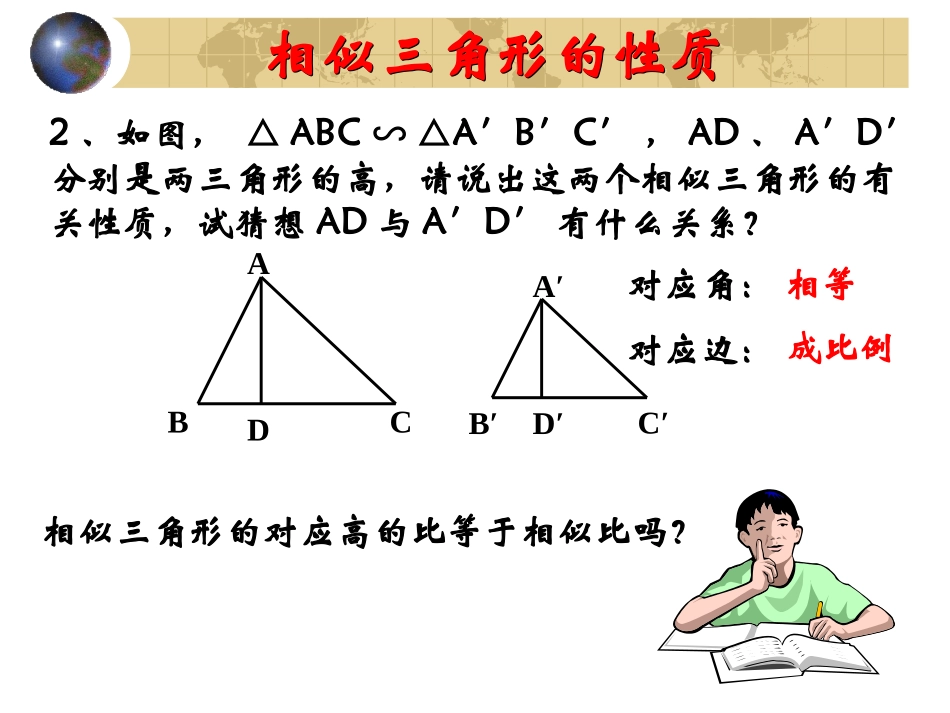
相似三角形的性质（1）相似三角形的性质（1）ABCD相似三角形的性质相似三角形的性质1、如图，△ABC≌△A′B′C′，AD、A′D′分别是两三角形的高，请说出这两个全等三角形的有关性质.A′B′C′D′对应角：对应边：对应边上的高：相等相等相等相似三角形的性质相似三角形的性质2、如图，△ABC∽△A′B′C′，AD、A′D′分别是两三角形的高，请说出这两个相似三角形的有关性质，试猜想AD与A′D′有什么关系？ABCDA′B′C′D′对应角：相等对应边：成比例对应边上的高：相似三角形的对应高的比等于相似比吗？相似三角形的性质相似三角形的性质ABCDA′B′C′D′证明：∵△ABC∽△A′B′C′，∴∠B=∠B′.又∵∠ADB=∠A′D′B′，∴△ABD∽△A′B′D′.kBAABDAAD已知：△ABC∽△A′B′C′，△ABC与△A′B′C′的相似比是k，AD、A′D′是对应高.求证：kDAAD中线ABCDA′B′C′D′角平分线ABCDA′B′C′D′定理：相似三角形对应高的比，对应中线的比和对应角平分线的比都等于相似比.定理：相似三角形对应高的比，对应中线的比和对应角平分线的比都等于相似比.相似三角形的性质相似三角形的性质例题例题例1如图，四边形ABCD中，AB=18，AC=12，AD=8，且∠ACB=ADC=90°∠，CEAB⊥，DF⊥AC，垂足分别为E、F.⑴求的值；⑵求证：CE=CD.DFCEABCDEF解：⑴∠ACB=ADC=90°∠，AB=18，AC=12，AD=8，,231218ACAB.23812ADAC,ADACACAB∴RtABCRtACD.△∽△又CEAB⊥，DFAC⊥，,23ACABDFCE（相似三角形的对应高的比等于相似比）⑵∵RtABCRtACD.△∽△∴∠BAC=CAD.∠又CEAB⊥，CDAD⊥，∴CE=CD变式练习11、已知：四边形ABCD中，AC平分∠DAB，∠ACD=A∠BC.求证：AC2=AB·AD.分析：△ABCACD∽△ACADABACAC2=AB·AD∠BAC=CAD∠，∠ABC=ACD∠（已知）（已知）B︶ACD⌒⌒变式练习2ABCDC′CABCCABCCDC′ABABABC上题中若把△ABC绕点A旋转，不论转到什么位置，上述结论是否成立？说明理由.⑴⑵小结小结小结小结1、相似三角形的性质对应角相等对应边成比例对应高的比，对应中线的比、对应角平分线的比都等于相似比.2、用符号语言填空：ABCDEFA′B′C′D′E′F′∵△ABCA′B′C′∽△，ADBC⊥，A′D′B′C′⊥，∴.BAABDAAD∵△ABCA′B′C′∽△，∠BAE=EAC∠，∠B′A′E′=E′A′C′∠，∴.BAABEAAE∵△ABCA′B′C′∽△，BF=CF，B′F′=C′F′，∴.BAABFAAF