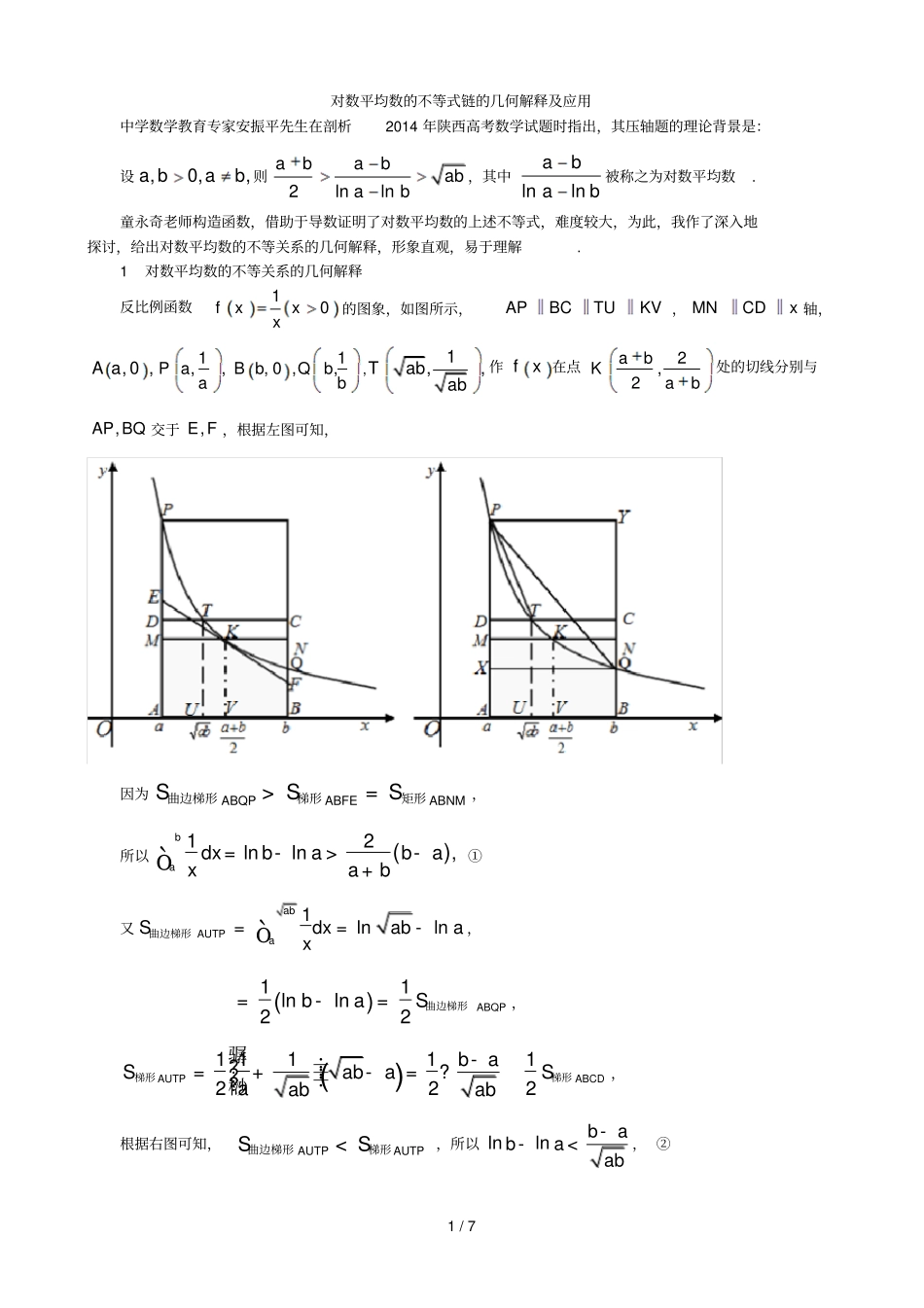
1/7对数平均数的不等式链的几何解释及应用中学数学教育专家安振平先生在剖析2014年陕西高考数学试题时指出,其压轴题的理论背景是:设,0,,abab则2lnlnabababab,其中lnlnabab被称之为对数平均数.童永奇老师构造函数,借助于导数证明了对数平均数的上述不等式,难度较大,为此,我作了深入地探讨,给出对数平均数的不等关系的几何解释,形象直观,易于理解.1对数平均数的不等关系的几何解释反比例函数10fxxx的图象,如图所示,APBCTUKV,MNCDx轴,,0,Aa1,,Paa1,0,,BbQbb,1,,Tabab作fx在点2,2abKab处的切线分别与,APBQ交于,EF,根据左图可知,因为ABNMABQPABFESSS>=矩形曲边梯形梯形,所以()12lnln,badxbabaxab=->-+ò①又1lnlnabAUTPaSdxabax==-ò曲边梯形,()11lnln22ABQPbaS=-=曲边梯形,()11111222AUTPABCDbaSabaSaabab骣-÷?=+-=?÷?÷?桫梯形梯形,根据右图可知,AUTPAUTPSS<曲边梯形梯形,所以lnlnbabaab--<,②2/7另外,ABQXABYPABQPABQPSSSS<<<矩形矩形曲边梯形梯形,可得:()()()11111lnln,2babababababa骣÷?-<-<+-<-÷?÷?桫③综上,结合重要不等式可知:()()()()211111lnln2bababababababababaab骣--÷?-<<-<<+-<-÷?÷?桫+,即()20112lnlnabbababababaab+->>>>>>>-+.④2不等式链的应用对数平均数的不等式链,提供了多种巧妙放缩的途径,可以用来证明含自然对数的不等式问题.对数平均数的不等式链包含多个不等式,我们可以根据证题需要合理选取其中一个达到不等式证明的目的.2.1()0lnlnbabaaba->>>-的应用例1(2014年陕西)设函数)1ln()(xxf,()()gxxfx,其中()fx是)(xf的导函数.(1)(2)(略)(3)设Nn,比较12gggn与nfn的大小,并加以证明.解析(3)因为1xgxx,所以1211112231231ngggnnnn,而ln1nfnnn,因此,比较12gggn与nfn的大小,即只需比较113121n与ln1n的大小即可.根据0ba>>时,lnlnbabba->-,即()1lnln,babab-<-令,1,anbn==+则()1ln1ln,1nnn<+-+所以1ln2ln1ln22,1ln3ln23,1,ln(1)ln1nnn,将以上各不等式左右两边相加得:111ln1231nn,3/7故12gggnnfn.评注本题是高考试题的压轴题,难度较大,为了降低试题的难度采取多步设问,层层递进,上问结论,用于下问,其第二问是为第三问做铺垫的“梯子”,尽管如此,步骤依然繁琐,求解过程复杂,但我们这里应用对数平均数不等式链来证明,思路简捷,别具新意,易于学生理解、掌握.当0ba>>时,lnlnbaaba->-,即()1lnln,babaa-<-令,1,anbn==+则()1ln1ln,nnn+-<可得:()111ln1123nn+<++++L.例2(2012年天津)已知函数ln0fxxxaa的最小值为0.(1)(2)(略)(3)证明:12ln212*.21ninnNi解析(3)易求1a,待证不等式等价于2222ln2135721nn.根据0ba>>时,lnlnbabba->-,即()1lnln,babab-<-令21,21,anbn=-=+则()()()22ln21ln21,21121nnnn=<+--+-+2ln3ln1,3<-2ln5ln3,5<-2ln7ln5,,7<-L()()()2ln21ln21,211nnn<+--+-将以上各不等式左右两边分别相加得:22222ln213572121nnn,122ln21222121ninin.得证.2.2()2202lnlnabbababa+->>>-的应用例3设数列na的通项111nann,其前n项的和为nS,证明:ln1nSn.4/7解析根据0ba>>时,222lnlnabbaba+->-,即()222lnlnbabaab-->+,令1,,bnan=+=则()()222ln1ln1nnnn+->++22221nn=++22222nann>>++,易证ln1nSn.2.3()02lnlnabbababa+->>>-的应用例4设数列na的通项111123nan,证明:ln21nan.解析根据0ba>>时,2lnlnabbaba+->-,即()2lnlnbabaab-->+,令21,21,bnan=+=-则()()1ln21ln21nnn+-->,易证ln21nan.2.4()2011lnlnbababaab->>>-+的应用例5(2010年湖北)已知函数()()0bfxaxcax=++>的图象在点()()1,1f处的切线方程为1yx=-.(1)用a表示出,bc;(2)(略)(3)证明:()()()1111ln11.2321nnnnn++++>++?+L解析(1)1,12baca=-=-;(3)当0ba>>时,211lnlnbabaab->-+,即()111lnln2babaab骣÷?-<+-÷?÷?桫,令,1,anbn==+则()111ln1ln,21nnnn骣÷?+-<+÷?÷?桫+所以111ln2ln1,212骣÷?-<+÷?÷?桫111ln3ln2,223骣÷?-<+÷?÷?桫L,5/7()111ln1ln,21nnnn骣÷?+-<+÷?÷?桫+将以上各不等式左右两边分别相加得:()()111111ln1,223421nnn骣÷?+<++++++÷?÷?桫+L即()()111111ln11,...