修改版七上第三章复习VIP免费

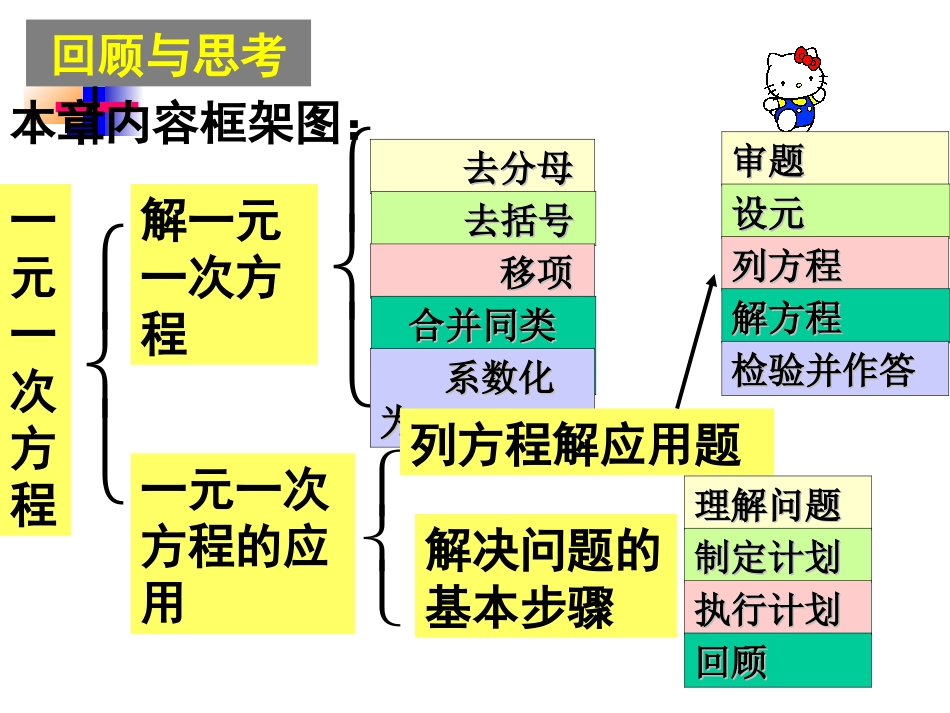
回顾与思考本章内容框架图：一元一次方程解一元一次方程一元一次方程的应用去分母去分母去括号去括号移项移项合并同类合并同类项项系数化系数化为为11列方程解应用题审题审题设元设元列方程列方程解方程解方程检验并作答检验并作答解决问题的基本步骤理解问题理解问题制定计划制定计划执行计划执行计划回顾回顾什么叫方程？含有未知数的等式叫做方程。注意：判断一个式子是不是方程，要看两点：一是等式；二是含有未知数。二者缺一不可。知识回顾判断下列各式哪些是方程，哪些不是？为什么？否是否是是是1、3-2=12、5x-1=93、y=04、x2+2x+15、3x-y=06、x2=5x-6典例分析11方程的基本变形法则(等式基本性质)是什么？(1)方程两边都加上或都减去同一个数或同一个整式，方程的解不变.（2）方程两边都乘以或都除以同一个不为零的数，方程的解不变。什么叫方程的解？使方程左右两边的值相等的未知数的值叫做方程的解.求方程的解的过程叫解方程。什么叫移项？将方程中的某些项改变符号后，从方程的一边移到另一边的变形叫做移项。※注意：移项一定要变号。大家判断一下，下列方程的变形是否正确？为什么？;2,021yy得由.32,23xx得由;47,47xx得由;35,53xx得由（1）（2）（3）（4）（×）（×）（×）（×）典例分析221.什么是一元一次方程？2.一元一次方程的一般式是什么？只含有一个未知数，并且含有未知数的式子都是整式，未知数的次数是1，这样的方程叫做一元一次方程.ax+b=0(a≠0,a、b为常数）1.判断下列方程是否为一元一次方程？为什么？（1）（5）（3）012x03x22xx067yx0122xx1232y（4）（2）（6）否否否否是是典例分析332.若是一元一次方程，则05374nxn。3.若方程是一元一次方程，则应满足633xxaa。4.若是方程1xaxxax523的解，则代数式2004a。21a≠31.下列方程中属于一元一次方程的是（）Ay2=4B2+1.下列方程中属于一元一次方程的是（）Ay2=4B2+2y2y=0Cx2+x+1=0Dx-2y=1=0Cx2+x+1=0Dx-2y=12.下列方程的解是2的是（）A.x+5=1-2xB.5x-3=0C.x-2=0D.x-2y=12.下列方程的解是2的是（）A.x+5=1-2xB.5x-3=0C.x-2=0D.x-2y=13.如果2xa+1+3=0是关于x的一元一次方程，则-a2+2a的值是（）3.如果2xa+1+3=0是关于x的一元一次方程，则-a2+2a的值是（）A.0B.2C.3D.4A.0B.2C.3D.44.解方程：4(x+0.5)=x+74.解方程：4(x+0.5)=x+7解：去括号得：4X+2=X+7移项得：4X-X=7-2合并得：3X=5系数化为1：X=解：去括号得：4X+2=X+7移项得：4X-X=7-2合并得：3X=5系数化为1：X=53BBCCAA当堂测试113.如果单项式是同类项，那么m=,n=.4.如果是关于X的一元一次方程，则a=1233mabc1(2)45aax132nabc解一元一次方程的一般步骤是什么？（1）去分母（2）去括号（3）移项（4）合并同类项（5）系数化为1①不能漏乘不含分母的项。②分子是多项式时应添括号。①不要漏乘括号内的任何项。②如果括号前面是“－”号，去括号后括号内各项变号。①从方程的一边移到另一边注意变号。①把方程一定化为ax=b(a≠0)的形式②系数相加，字母及其指数不变。①方程两边除以未知数的系数。②系数只能做分母，注意不要颠倒。32523xx解：)2(5)23(3xx10569xx61059xx164x4x典例分析44143652yy解：1233522yy1239104yy9101234yy13y变式训练11解：)1(2)]1(21[23xxx22]2121[23xxx22)2121(23xx224343xx432243xx41145x511x变式训练22用适当的方法解下列方程32(1)[(1)2]2234212(21)5(21)(2)40236xxxxx.)20063(20077,23)20063(5的值求代数式已知xx1200635)20063(532)20063(5xxx解：2000120077)20063(20077x35.0102.02.01.0xx解：5101022010xx＝330)1010(2)2010(5xx30202010050xx20100302050xx15030x5x变式训练33方程的定义方程的基本变形法则方程移项一元一次方程一元一次方程的概念解一元一次方程的一般...