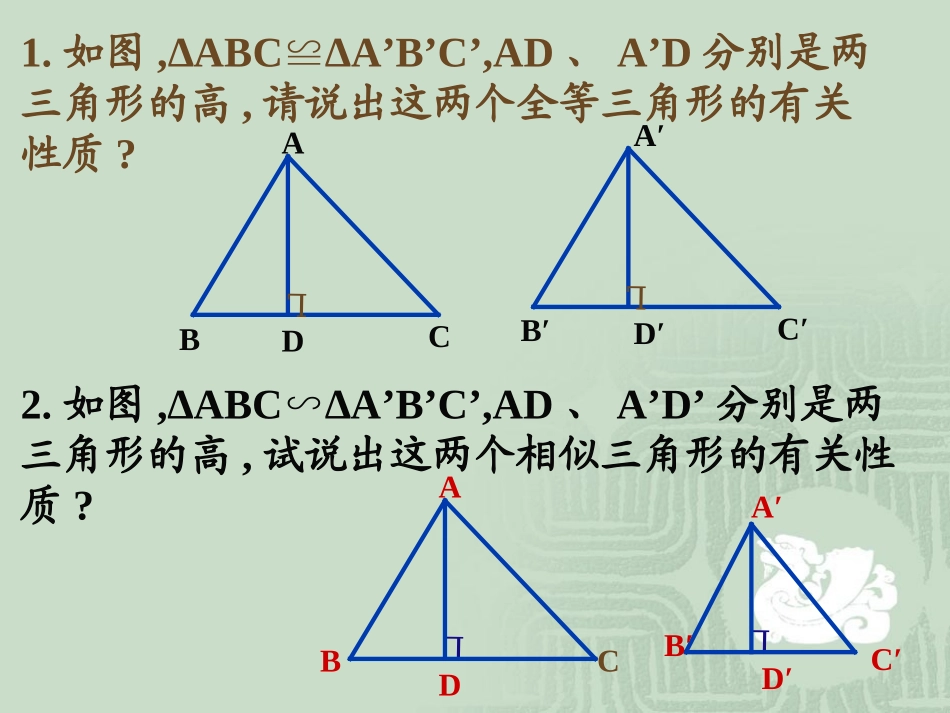
ⅬABCDⅬA′B′C′D′1.如图,∆ABC∆A’B’C’,AD≌、A’D分别是两三角形的高,请说出这两个全等三角形的有关性质?ⅬⅬABCDA′B′C′D′2.如图,∆ABC∆A’B’C’,AD∽、A’D’分别是两三角形的高,试说出这两个相似三角形的有关性质?定理1:相似三角形对应高的比,对应中线的比,对应角平分线的比都等于相似比。相似三角形的性质例题【例1】.如图已知△ABCA’B’C’∽△中,AE,A’E’是对应中线,求证:△ACDA’C’D’∽△EE’练习【练1】.如图已知△ABCA’B’C’∽△中,AF,A’F’是对应角平分线,求证:△ABDA’B’D’∽△。AA’BB’CC’F’F1.如果两个相似三角形的对应高的比为2:3,那么对应角平分线的比是__,对应边上的中位线的比是______。2.如果两相似三角形的对应边上的中线的比为1:2,那么对应边上高的比是____。3.△ABC与△A'B'C'的相似比为1:3,若BC=5cm,则B'C'=_____。2:32:31:215cm4.△ABC与△A'B'C'的相似比为2:5,若A'C'=10cm,则AC=_____5.△ABC与△A'B'C'的相似比为3:4,若BC边上的高AD=12cm,则B'C'边上的高A'D'=_____。4cm16cm6.△ABC与△A’B’C’的相似比为1:5,如果A’C’边上的中线B’D’=20cm,则AC边上的中线BD=____。7.顺次连结三角形三边中点所成的三角形与原三角形对应高的比是______。8.如图(5)ABCA’B′C′△∽△,对应中线AD=6cm,A’D’=10cm,若BC=4.2cm,则B’C′=______。4cm1:27cm相似三角形的性质(特别注意“对应”二字)对应角相等对应边成比例对应高的比、对应中线的比、对应角平分线的比都等于相似比.ⅬABCDEFⅬA′B′C′D′E'F'1.两个相似三角形对应高的比为3:5,则对应角平分线的比为_____。2.两个相似三角形对应中线的比为1:4,则对应高的比为______。3.△ABC与△A’B’C’的相似比为4:7,若BC边上的中线AD=8cm,则B’C‘边上的中线A’D’=___。4.△ABC与△A’B’C’的相似比为2:3,若BC边上的中线AD=8cm,则B’C’边上的中线A’D’=.5.△ABC与△A'B'C'的相似比为3:2,若角平分线A'D'=4cm,则角平分线AD=_____。3:51:414126