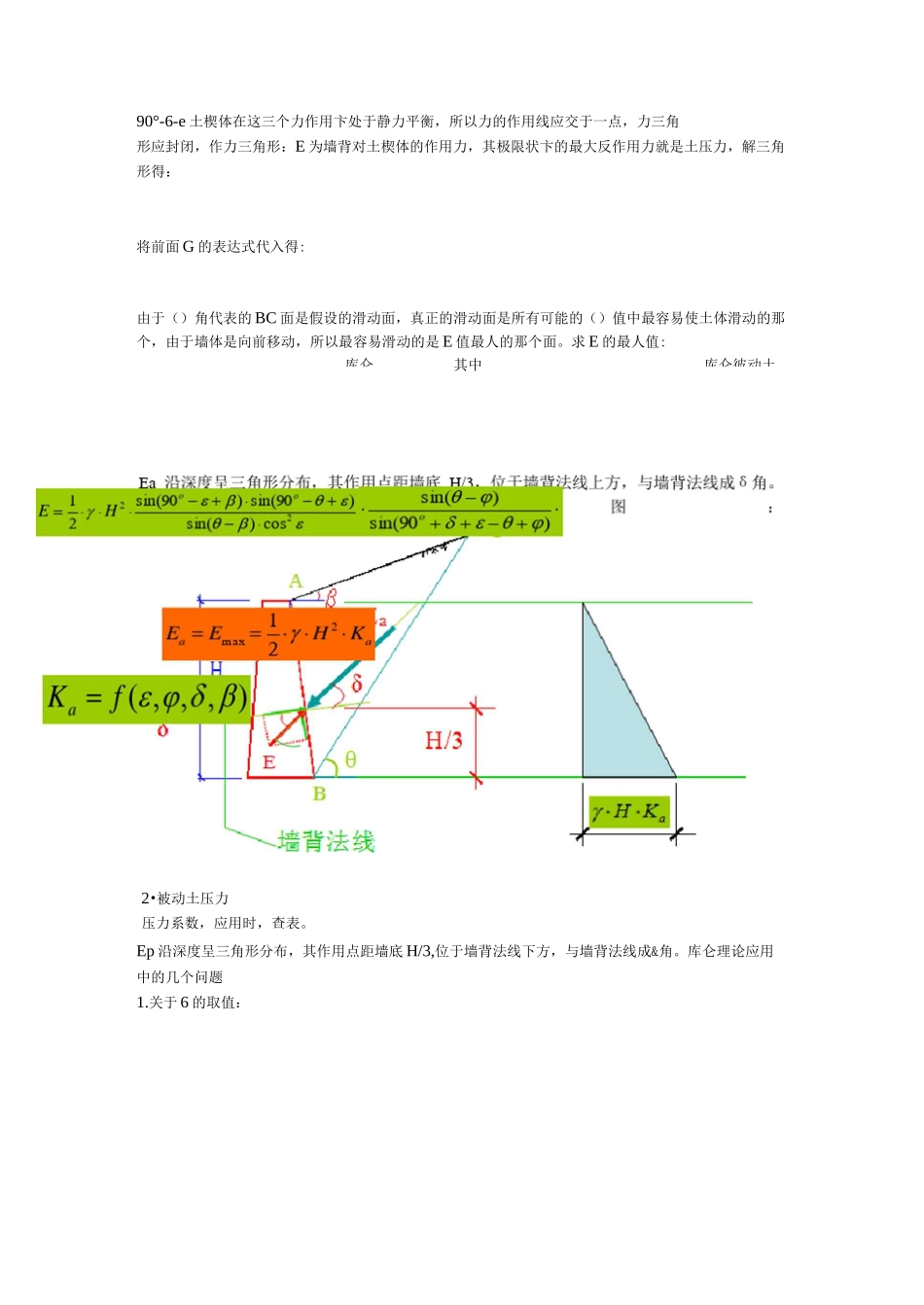
为摩擦系",据的作(3)用厂]rrnrr2-C"一疑法EpJ.y.Hh卄2・c・H590°-c_l“sin(90。一£+0)・sin(9(r-&+£)韋挡土墙:;/H'sm(e_0)cos订片体对墙背的作用力称为土压力。-、三种土压加以分为三种类型:1.主动土压力Ea一一在土压力作用下,挡土墙发生离开土体方向的位移,墙后填土达到极限平衡状态,此时墙背上的土压力称为主动土压力,记为Ea。2.被动土压力Ep一一在外力作用下,挡土墙发生挤向土体方向的位移,墙后填土达到极限平衡状态,此时墙背上的土压力称为被动土压力,记为Ep。3.静止土压力Eo一一墙土间无位移,墙后填土处于弹性平衡状态,此时墙背上的土压力称为静止土压力,记为Eo。二、三种土压力在数量上的关系墙、土间无位移,墙后填土处于弹性平衡状态,与天然状态相同,此时的土压力为静止土压力;在此基础上,墙发生离开土体方向的位移,墙、土间的接触作用减弱,墙、土间的接触压力减小,因此主动土压力在数值上将比静止土压力小:而被动土压力是在静止土压力的基础上墙挤向土体,随着墙、土间挤压位移量的越大,因此被动土压力最大。即:Ea',4),为土的有效内摩擦角。H为挡土墙高度,m。朗肯土压力理一1857年,朗肯根据半空间应力状态下的极限平衡条件导出了土压力的计算公式;称为朗肯土压力理论。1•主动土压力Eam——朗肯主动土压力系数;c——填土的内聚力,(kPa);挡土墙墙高为H,墙后填土的容重为Y,内摩擦角为“。(对于砂土c=0)2.被动土压力Ep1/m朗肯被动土压力系数:库仑土压力理论一墙离开或挤向土体时的极限状态下,墙后形成一具有滑动趋势的土楔体,根据该土楔体的静力平衡条件求解。假设:墙后填土是理想的无粘性土,滑裂面为过墙踵的平面。1.主动土压力(1)土楔体自重G(2)滑动面EC上的作用力R—一主动状态,墙向前移动,土楔体下滑,摩擦力向上,EC面上总的摩擦力与法向力之和为R,按物理学:f=u.Ntan(45"+2•被动土压力压力系数,应用时,查表。其中库仑彼动土90°-6-e土楔体在这三个力作用卞处于静力平衡,所以力的作用线应交于一点,力三角形应封闭,作力三角形:E为墙背对土楔体的作用力,其极限状卞的最大反作用力就是土压力,解三角形得:将前面G的表达式代入得:由于()角代表的BC面是假设的滑动面,真正的滑动面是所有可能的()值中最容易使土体滑动的那个,由于墙体是向前移动,所以最容易滑动的是E值最人的那个面。求E的最人值:Ep沿深度呈三角形分布,其作用点距墙底H/3,位于墙背法线下方,与墙背法线成&角。库仑理论应用中的几个问题1.关于6的取值:库仑=1/2〜1/3Ep=EminRJL)一疋1也丁K二各午■析解|与N之间的夹角"D—定大于R与N之间的夹角“,鉴于6值与墙后填土的性质、填土含水量及墙背的粗糙程度变化于0〜e之间,实用中常取6此,实用中,可考虑将粘性土的e值适当增人,用增大后的Ae来近似考虑c值对土压力的影响。3.库仑理论和朗肯理论间的差异一一库仑理论是利用土楔体在极限状态的静力平衡条件求解,朗肯理论应用的是半空间应力状态下的极限平衡关系式。两者的出发点不同;在库仑公式中,若6=0(墙背光滑)、£=0(墙背垂直、B=0(填土面水平),贝IJ库仑理论的Ka=tair(45-4)/2),即朗肯理论可以看成是库仑理论当6=0.£=0、B=0时的特例。4.关于滑动面的形状一一理论推导时,假设滑动面EC是平面,而实际上是一曲面:主动状态墙向前移,真正的滑动面接近于圆弧(筒)面,当半径较人时,基本上可以看成是平面,因而,按平面计算,其误差相对较小,约为2〜10%,尚可以满足工程要求;故工程上,主动土压力一般可以按库仑土理论计算;而在被3•局部均布荷载作用墙背垂直、光滑时0=45+(1>/2在a点以上,点之间,按直线处理。动状态,墙挤向土不考be在口:力:亠口HuFFl.日丄苗心Q苗IfflE口亠由中Y・z项仍取计算点处的自重应力,其计算点处的c、e按4就按哪层土取用,在两层土Pa3山2)・朮一2・C2・Nt2分别求面积后、叠加,即得所求土压力。hi%h£三、墙后填土有地下水时=tan(45"—号)=tan(45"—^―)=0.70m...