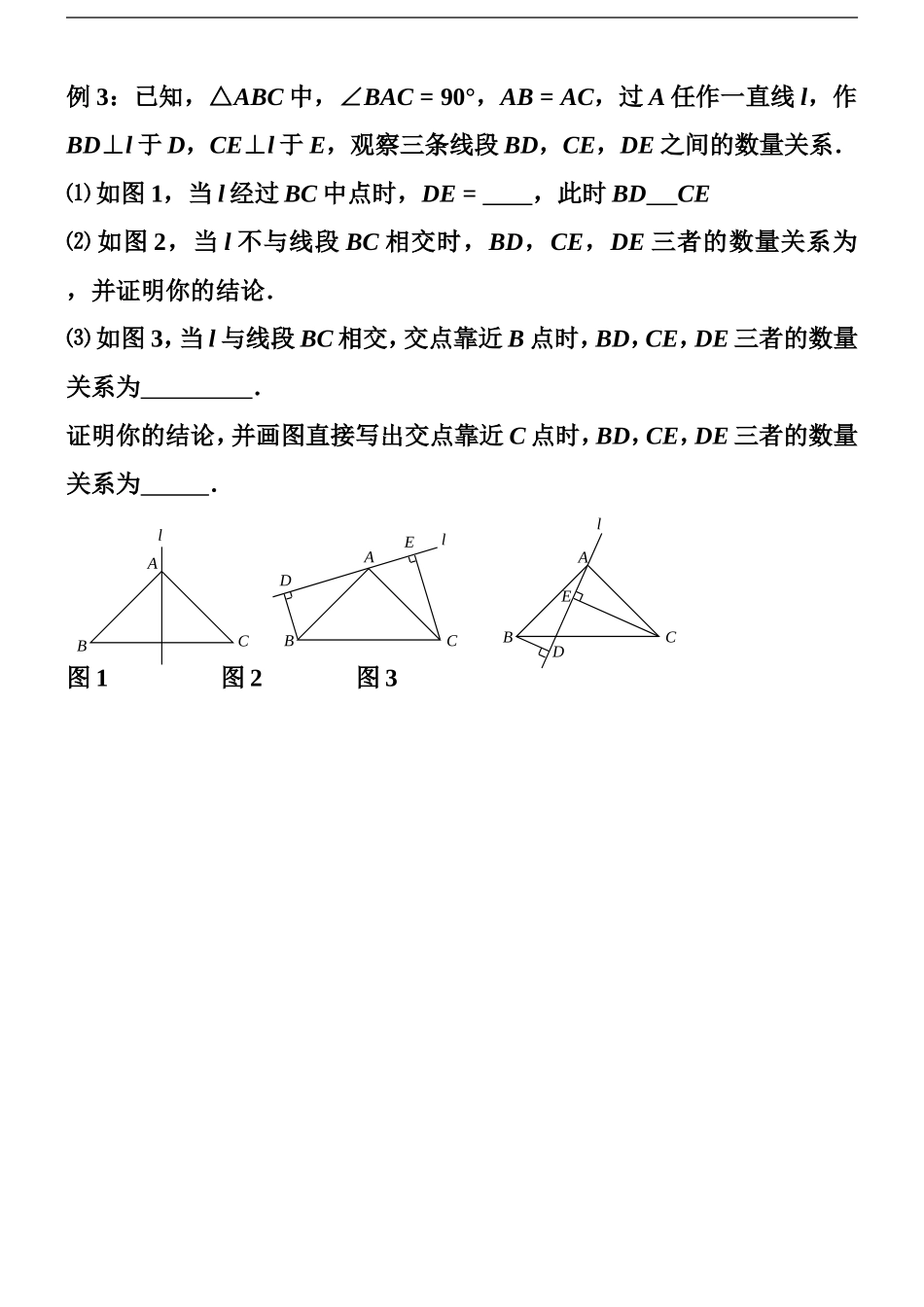
全等三角形典型例题:例1:(2014威海)把两个含有45°角的直角三角板如图1放置,点D在BC上,连结BE,AD,AD的延长线交BE于点F.求证:AF⊥BE.练习1:如图,在△ABC中,∠BAC=90°,AB=AC,AE是过点A的直线,BD⊥AE,CE⊥AE,如果CE=3,BD=7,请你求出DE的长度。例2:△DAC,△EBC均是等边三角形,AE,BD分别与CD,CE交于点M,N,求证:(1)AE=BD;(2)CM=CN;(3)△CMN为等边三角形;(4)MN∥BC。AFBCEDEDACBEEEDACBNM例3:已知,△ABC中,∠BAC=90°,AB=AC,过A任作一直线l,作BD⊥l于D,CE⊥l于E,观察三条线段BD,CE,DE之间的数量关系.⑴如图1,当l经过BC中点时,DE=,此时BDCE⑵如图2,当l不与线段BC相交时,BD,CE,DE三者的数量关系为,并证明你的结论.⑶如图3,当l与线段BC相交,交点靠近B点时,BD,CE,DE三者的数量关系为.证明你的结论,并画图直接写出交点靠近C点时,BD,CE,DE三者的数量关系为.图1图2图3AlBCABCDElABClEDOyABCxOyABCDEx例4:已知:在平面直角坐标系中,放入一块等腰直角三角板ABC,∠BAC=90°,AB=AC,A点的坐标为(0,2),B点的坐标为(4,0).⑴求C点的坐标;⑵D为△ABC内一点(AD>2),连AD,并以AD为边作等腰直角三角形ADE,∠DAE=90°,AD=AE,连CD、BE.试判断线段CD、BE的位置及数量关系,并给出你的证明;OyABCDEMx⑶旋转△ADE,使D点刚好落在x轴的负半轴,连CE交y轴于M.求证:①EM=CM;②BD=2AM.练习2:以直角三角形ABC的两直角边AB、BC为一边,分别向外作等边三角形△ABE和等边△BCF,连结EF、EC。试说明:(1)EF=EC;(2)EB⊥CFCBAFE练习3:如图(1)A、E、F、C在同一直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC若AB=CD,G是EF的中点吗?请证明你的结论。若将⊿ABC的边EC经AC方向移动变为图(2)时,其余条件不变,上述结论还成立吗?为什么?例5:如图1,已知,AC⊥CE,AC=CE,∠ABC=∠CDE=90°,问BD=AB+ED吗?[变形1]:如图2,如果△ABC≌△CDE,请说明AC与CE的关系。BDECA图1BDECA图2[变形2]:(2014泸州)如图,E是正方形ABCD的边DC上的一点,过点A作FA⊥AE交CB的延长线于点F,求证:DE=BF[变形3]:如图3,在△ABC中,∠BAC=90°,AB=AC,AE是过点A的直线,BD⊥AE,CE⊥AE,如果CE=3,BD=7,请你求出DE的长度。[变形4]:在△ABC中,∠ACB=900,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。(1)当直线MN绕点C旋转到图4的位置时,△ADC≌△CEB,且DE=AD+BE。你能说出其中的道理吗?EDACB图31EDACB图4FABDCE(2)当直线MN绕点C旋转到图5的位置时,DE=AD-BE。说说你的理由。(3)当直线MN绕点C旋转到图6的位置时,试问DE,AD,BE具有怎样的等量关系?请写出这个等量关系。等腰三角形、等边三角形的全等问题:[必备知识]:如右图,由∠1=∠2,可得∠CBE=∠DBA;反之,也成立。例6:已知在△ABC中,AB=AC,在△ADE中,AD=AE,且∠1=∠2,请问BD=CE吗?2ACBED1图13图6EDCBANM图6EDCBANMEDCBANM图512BCAED[变形1]:如图13,已知∠BAC=∠DAE,∠1=∠2,BD=CE,请说明△ABD≌△ACE.吗?为什么?[变形2]:过点A分别作两个大小不一样的等边三角形,连接BD,CE,请说明它们相等。DCBAE图1521图13_A_C_B_E_D[变形3]:如图16—18,还是刚才的条件,把右侧小等边三角形的位置稍加变化,,连接BD,CE,请说明它们相等DCBAE图18DCBAEDCBAEDCBAEDCBAE图16DCBAE图17[变形4]:(2014怀化)如图,四边形ABCD、DEFG都是正方形,连接AE、CG,AE与CG相交于点M,CG与AD相交于点N.求证:;例四:如图,△ABC中,∠C=90°,AB=2AC,M是AB的中点,点N在BC上,MN⊥AB.求证:AN平分∠BAC.[变形]:在Rt△ABC中,已知∠A=90°,DE⊥BC于E点,如果AD=DE,BD=CD,求∠C的度数ABGDFECDEBACBCNMA