11回归分析的基本思想及其初步应用3VIP免费

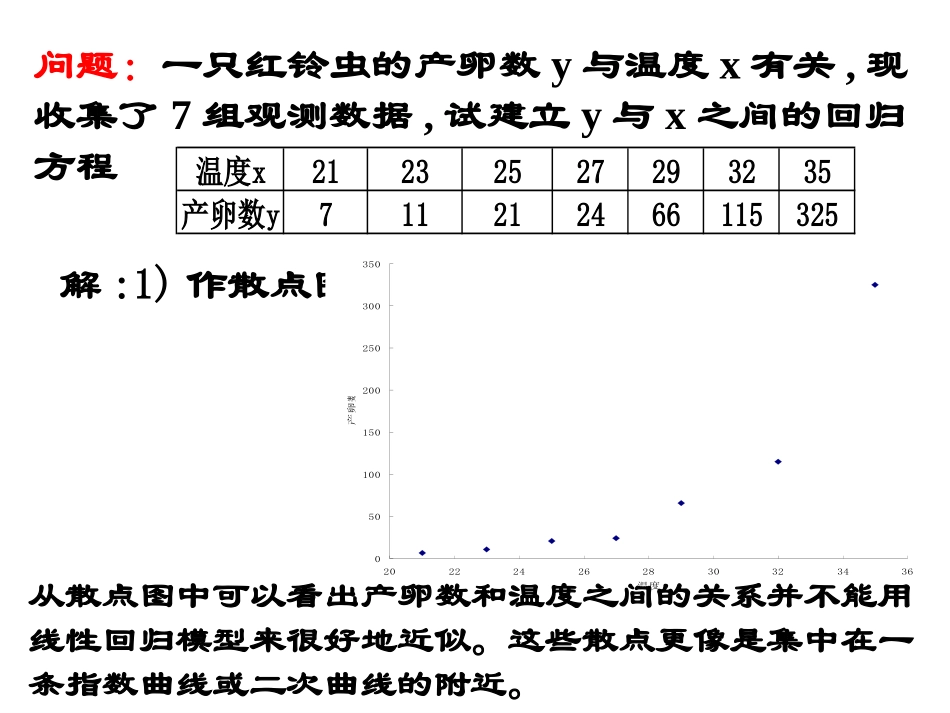
1)确定解释变量和预报变量;2)画出散点图;3)确定回归方程类型;4)求出回归方程;5)利用相关指数或残差进行分析.建立回归模型的基本步骤问题：一只红铃虫的产卵数y与温度x有关,现收集了7组观测数据,试建立y与x之间的回归方程温度x21232527293235产卵数y711212466115325解:1)作散点图;050100150200250300350202224262830323436温度产卵数从散点图中可以看出产卵数和温度之间的关系并不能用线性回归模型来很好地近似。这些散点更像是集中在一条指数曲线或二次曲线的附近。解:令则z=bx+a,(a=lnc1,b=c2),列出变换后数据表并画出x与z的散点图z=lnyx和z之间的关系可以用线性回归模型来拟合z=ax+b+e2cx1用y=ce模型;1)x21232527293235z1.9462.3983.0453.1784.194.7455.784z01234567010203040z2)用y=c3x2+c4模型,令,则y=c3t+c4,列出变换后数据表并画出t与y的散点图2t=x散点并不集中在一条直线的附近，因此用线性回归模型拟合他们的效果不是最好的。t44152962572984110241225y711212466115325y0501001502002503003500200400600800100012001400yˆˆ(1)0.272x-3.843(2)2y=e,y=0.367x-202.54ˆˆˆˆ(1)(1)0.272x-3.843iii(2)(2)2iiie=y-y=y-e,(i=1,2...7)e=y-y=y-0.367x+202.54,残差表编号1234567x21232527293235y711212466115325e(1)0.52-0.1671.76-9.1498.889-14.15332.928e(2)47.719.397-5.835-41.003-40.107-58.26877.965非线性回归方程二次回归方程残差公式在此处可以引导学生体会应用统计方法解决实际问题需要注意的问题：对于同样的数据，有不同的统计方法进行分析，我们要用最有效的方法分析数据。现在有三个不同的回归模型可供选择来拟合红铃虫的产卵数与温度数据，他们分别是：.,,212exyecyebaxyexc可以利用直观（散点图和残差图）、相关指数来确定哪一个模型的拟合效果更好。ebxcz2ety问题六：若两个变量呈现非线性关系，如何解决？（分析例2）例2一只红铃虫的产卵数y和温度x有关。现收集了7组观测数据列于表中：温度xoC21232527293235产卵数y/个711212466115325（1）试建立产卵数y与温度x之间的回归方程；并预测温度为28oC时产卵数目。（2）你所建立的模型中温度在多大程度上解释了产卵数的变化？选变量解：选取气温为解释变量x，产卵数为预报变量y。画散点图假设线性回归方程为：ŷ=bx+a选模型分析和预测当x=28时，y=19.87×28-463.73≈93估计参数由计算器得：线性回归方程为y=19.87x-463.73相关指数R2=r2≈0.8642=0.7464所以，一次函数模型中温度解释了74.64%的产卵数变化。050100150200250300350036912151821242730333639当x=28时，y=19.87×28-463.73≈93方法一：一元函数模型y=c1x2+c2变换y=c1t+c2非线性关系线性关系问题１选用y=c1x2+c2，还是y=c1x2+cx+c2？问题3-200-1000100200300400-40-30-20-10010203040产卵数气温问题2如何求c1、c2？t=x2方法二，二元函数模型平方变换：令t=x2，产卵数y和温度x之间二次函数模型y=bx2+a就转化为产卵数y和温度的平方t之间线性回归模型y=bt+a温度21232527293235温度的平方t44152962572984110241225产卵数y/个711212466115325作散点图，并由计算器得：y和t之间的线性回归方程为y=0.367t-202.54，相关指数R2=r2≈0.8962=0.802将t=x2代入线性回归方程得：y=0.367x2-202.54当x=28时，y=0.367×282-202.54≈85，且R2=0.802，所以，二次函数模型中温度解释了80.2%的产卵数变化。产卵数y/个0501001502002503003500150300450600750900105012001350t产卵数气温变换y=bx+a非线性关系线性关系43cxyce-50050100150200250300350400450-10-50510152025303540对数方法三：指数函数模型xccexccecyxc43433lnlnlnlnlnln4abxzzybcac则有令,ln,,ln43温度x/21232527Z=lny1.9462.3983.4053.178产卵数y/个71121242932354.1904.7455.78466115325c由计算器得：z关于x的线性回归方程相关指数因此y关于x的非线性回归方程为98.02R489.3272.0^xz当x=28时，y≈44，指数回归模型中温度解释了98%的产卵数的变化C489.3272.0^xey函数模型相关指数R2线性回归模型0.7464二次函数模型0.802指数函数模型...