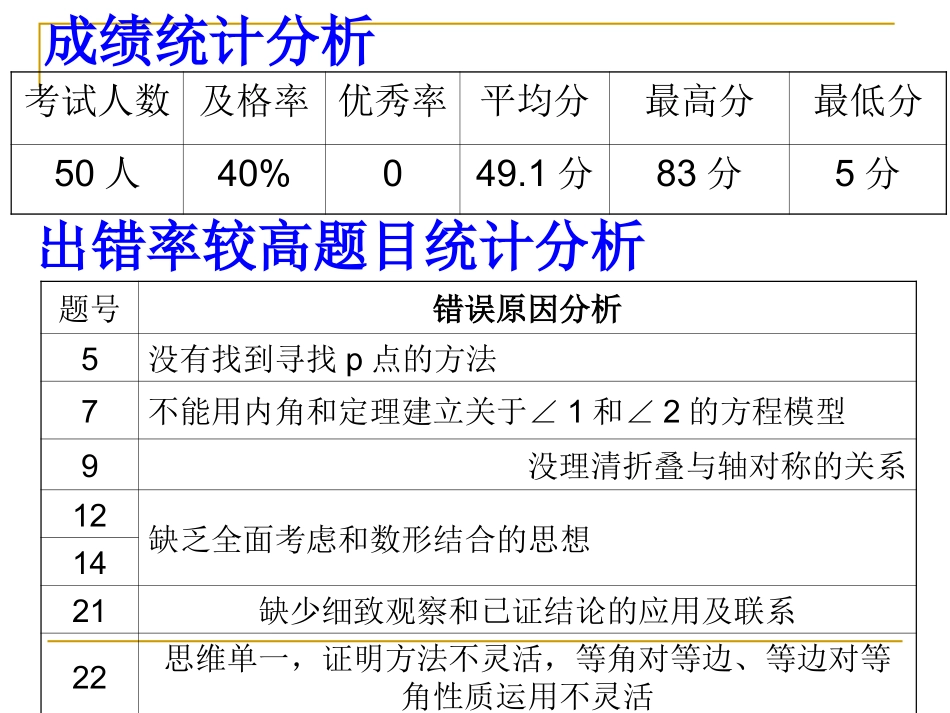
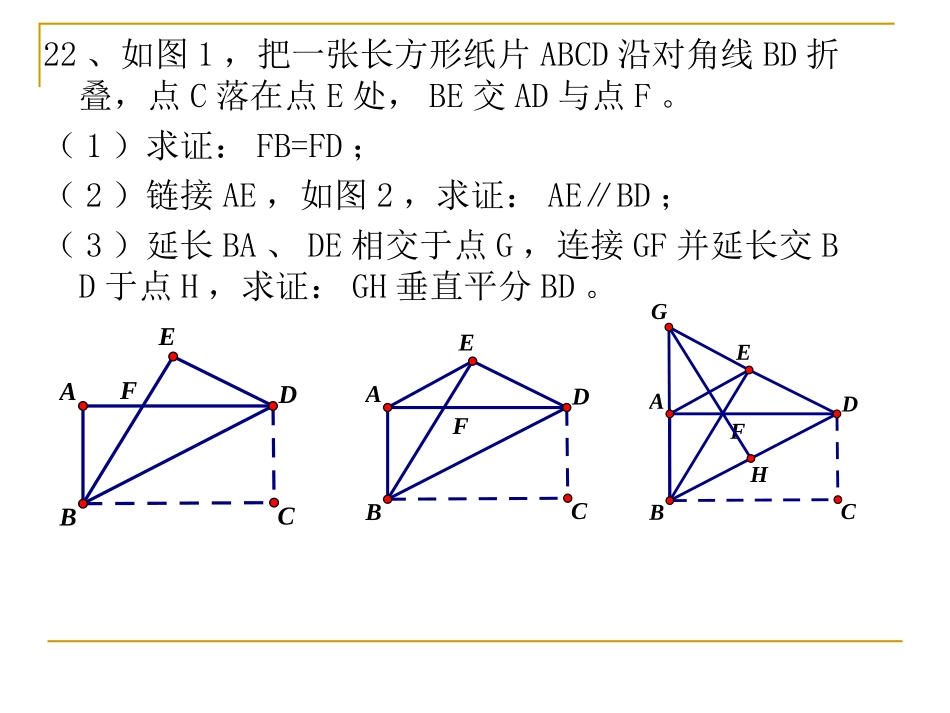
八年级上册数学期中试卷讲评金寨初中张道宪成绩统计分析考试人数及格率优秀率平均分最高分最低分50人40%049.1分83分5分出错率较高题目统计分析题号错误原因分析5没有找到寻找p点的方法7不能用内角和定理建立关于∠1和∠2的方程模型9没理清折叠与轴对称的关系12缺乏全面考虑和数形结合的思想1421缺少细致观察和已证结论的应用及联系22思维单一,证明方法不灵活,等角对等边、等边对等角性质运用不灵活22、如图1,把一张长方形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD与点F。(1)求证:FB=FD;(2)链接AE,如图2,求证:AE∥BD;(3)延长BA、DE相交于点G,连接GF并延长交BD于点H,求证:GH垂直平分BD。FABDCEFABDCEFABDCEGH22.(1)证明:由图中折叠可知:∠EBD=DBC∠∵在长方形ABCD中,ADBC∥∴∠DBC=ADB∠∴∠EBD=ADB∠∴FB=FD(等角对等边)(2)在长方形ABCD中,AD=BC有折叠可知,BC=BE,故AD=BE。由(1)知BF=FD,∴AD-BF=BE-BF,即AF=EF∴∠FAE=AEF∠又∵由(1)已证∠FBD=FDB∠∴∠EFD=2EAD=2FDB∠∠∴∠EAD=FDBAEBD∠∴∥(3)在长方形ABCD中,ABCD∥,故∠ABD=BDC∠再由折叠可知,∠BDC=GDB∠,故∠ABD=GDBGB=GD∠∴∴点G在BD的垂直平分线上。又∵FB=FD∴点F在BD的垂直平分线上,∴GF是BD的垂直平分线,即GH垂直平分BD。21、如图,C是线段BE上一点,以BC、CE为边分别在BE的同侧作等边△ABC和等边△DCE,连结AE、BD。(1)求证BD=AE。(2)若M、N分别是线段AE、BD上的点,且AM=BN,请判断△CMN的形状,并说明理由。ABCED图(1)MNABCED图(2)21.(2)△CMN为等边三角形。证明:由(1)△BCDACE≌△可得:∠CAE=DBC∠。在△AMC和△BNC中AM=BN∠CAE=DBC∠AC=BC∴△AMCBNC≌△(SAS)∴CM=CNACM=BCN∠∠又∵∠BCN+ACN=ACB=60°∠∠∴∠ACM+ACN=60°∠即∠MCN=60°∴△MCN是等边三角形。变式练习一1、如图所示,△ABC和△CDE均为等边三角形,AC和CE不在同一直线上,连接AE,BD。试判断AE与BD的关系,并说明理由。ACDEB2、如图,C是线段BE上一点,以BC、CE为边分别在BE的同侧作等边△ABC和等边△DCE,连接AE、BD。若AE交CD于M,BD交AC于N,连接MN,试判断△CMN的形状,并说明理由。AEMNDCB变式练习二选择作业,深化提升1、60分以下的同学将没有具体讲解的错题纠正,选择填空有过程需写过程,并纠正主观性试题。2、60分以上的同学在前一层次基础上,把本节集体讲评的每个题目,写出规范合理的解答过程,并完成课后拓展。如图:四边形ABCD和DEFG都是正方形,连接AE,CG。(1)求证:AE=CG(2)观察图形,猜想AE与CG有什么位置关系,并证明你的猜想。AMNGFEDCB