中考几何应用题VIP免费

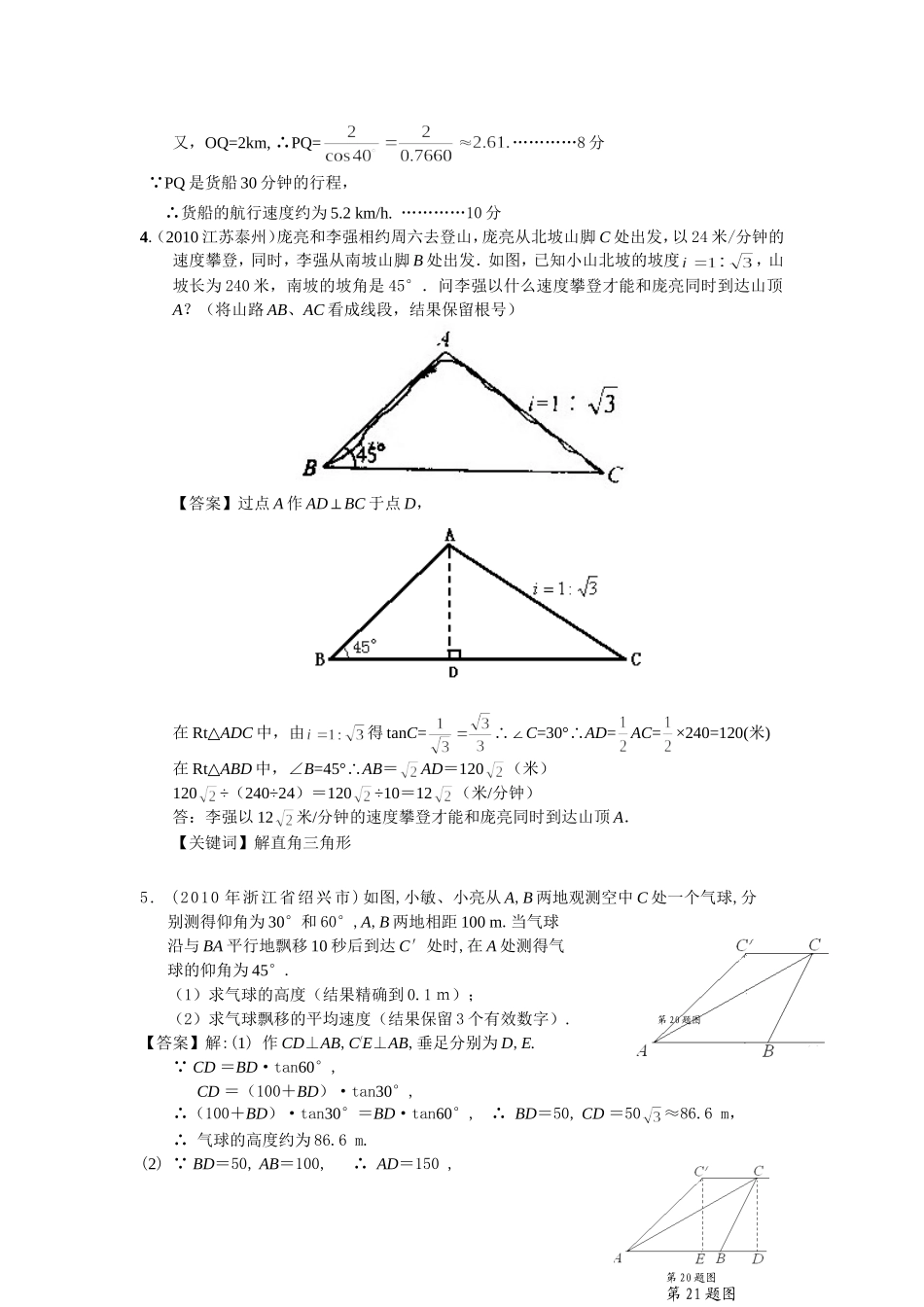
中考几何应用题集锦1.（2010年福建省晋江市）已知：如图，有一块含30的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等，把该套三角板放置在平面直角坐标系中，且3AB.(1)若双曲线的一个分支恰好经过点A，求双曲线的解析式；(2)若把含30的直角三角板绕点O按顺时针方向旋转后，斜边OA恰好与x轴重叠，点A落在点A，试求图中阴影部分的面积(结果保留).答案：解：(1)在OBARt中，30AOB，3AB，ABOBAOBcot，∴3330cotABOB，∴点33,3A设双曲线的解析式为0kxky∴333k，39k，则双曲线的解析式为xy39(2)在OBARt中，30AOB，3AB，OAABAOBsin，OA330sin，∴6OA.由题意得：60AOC，63606602'AOAS扇形在OCDRt中，45DOC，33OBOC，∴263223345cosOCOD.∴427263212122ODSODC.∴'27S64ODCAOASS阴扇形＝AOABCDA’xAyxAAOABCDA’xAyxA2.（2010年青岛）小明家所在居民楼的对面有一座大厦AB，AB＝米．为测量这座居民楼与大厦之间的距离，小明从自己家的窗户C处测得大厦顶部A的仰角为37°，大厦底部B的俯角为48°．求小明家所在居民楼与大厦的距离CD的长度．（结果保留整数）（参考数据：）【答案】解：设CD=x．在Rt△ACD中，，则，∴.在Rt△BCD中，tan48°=，则，∴. AD＋BD=AB，∴．解得：x≈43．3.(2010年福建省德化县).(本题满分10分)小明在某风景区的观景台O处观测到北偏东的P处有一艘货船,该船正向南匀速航行,30分钟后再观察时,该船已航行到O的南偏东40,且与O相距2km的Q处.如图所示.求:(1)∠OPQ和∠OQP的度数;(2)货船的航行速度是多少km/h?(结果精确到0.1km/h,已知sin=cos=0.7660,cos=sin=0.6428,tan=1.1918,tan=0.8391,供选用.)【答案】解:建立如图所示的直角坐标系,(1)设PQ⊥x轴,垂足为A,则∠POA=,∠QOA=.……2分∴∠OPQ=，∠OQP=．…………4分(2)设货船的航行速度是xkm/h,由（1）知，∠POQ=.……5分∴cos∠OQP=.∴PQ=.…………7分AB37°48°DCA第19题图又，OQ=2km,∴PQ=…………8分 PQ是货船30分钟的行程，∴货船的航行速度约为5.2km/h.…………10分4.（2010江苏泰州）庞亮和李强相约周六去登山，庞亮从北坡山脚C处出发，以24米/分钟的速度攀登，同时，李强从南坡山脚B处出发．如图，已知小山北坡的坡度，山坡长为240米，南坡的坡角是45°．问李强以什么速度攀登才能和庞亮同时到达山顶A？（将山路AB、AC看成线段，结果保留根号）【答案】过点A作AD⊥BC于点D，在Rt△ADC中，由得tanC=∴∠C=30°∴AD=AC=×240=120(米)在Rt△ABD中，∠B=45°∴AB＝AD＝120（米）120÷（240÷24）＝120÷10＝12（米/分钟）答：李强以12米/分钟的速度攀登才能和庞亮同时到达山顶A．【关键词】解直角三角形5.(2010年浙江省绍兴市)如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为30°和60°,A,B两地相距100m.当气球沿与BA平行地飘移10秒后到达C′处时,在A处测得气球的仰角为45°.（1）求气球的高度（结果精确到0.1ｍ）；（2）求气球飘移的平均速度（结果保留3个有效数字）.【答案】解:(1)作CD⊥AB,C/E⊥AB,垂足分别为D,E. CD＝BD·tan60°,CD＝（100＋BD）·tan30°,∴（100＋BD）·tan30°＝BD·tan60°,∴BD＝50,CD＝50≈86.6m，∴气球的高度约为86.6m.(2) BD＝50,AB＝100,∴AD＝150,第20题图第20题图第21题图又 AE＝C/E＝50,∴DE＝150－50≈63.40，∴气球飘移的平均速度约为6.34米/秒.6.（2010年宁德市）我们知道当人的视线与物体表面互相垂直时的视觉效果最佳．如图是小明站在距离墙壁1.60米处观察装饰画时的示意图，此时小明的眼睛与装饰画底部A处于同一水平线上，视线恰好落在装饰画中心位置E处，且与AD垂直.已知装饰画的高度AD为0.66米，求：⑴装饰画与墙壁的夹角∠CAD的度数（精确到1°）；⑵装饰画顶部到墙壁的距离DC（精确到0.01米）.【答案】解：⑴ AD＝0.66，∴AE＝CD＝0.33.在Rt△ABE中， sin∠ABE＝＝，∴∠ABE≈12°. ∠CAD＋∠DAB＝90°，∠ABE＋∠DAB＝90°，∴∠CAD＝∠ABE＝12°.∴镜框与墙壁的...