定积分的概念VIP免费

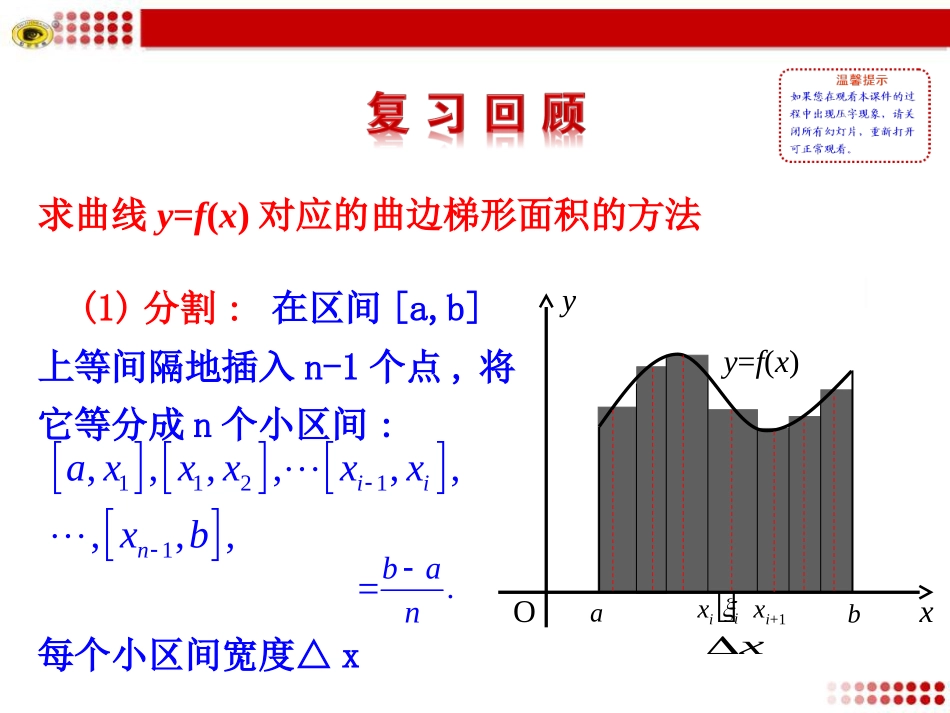
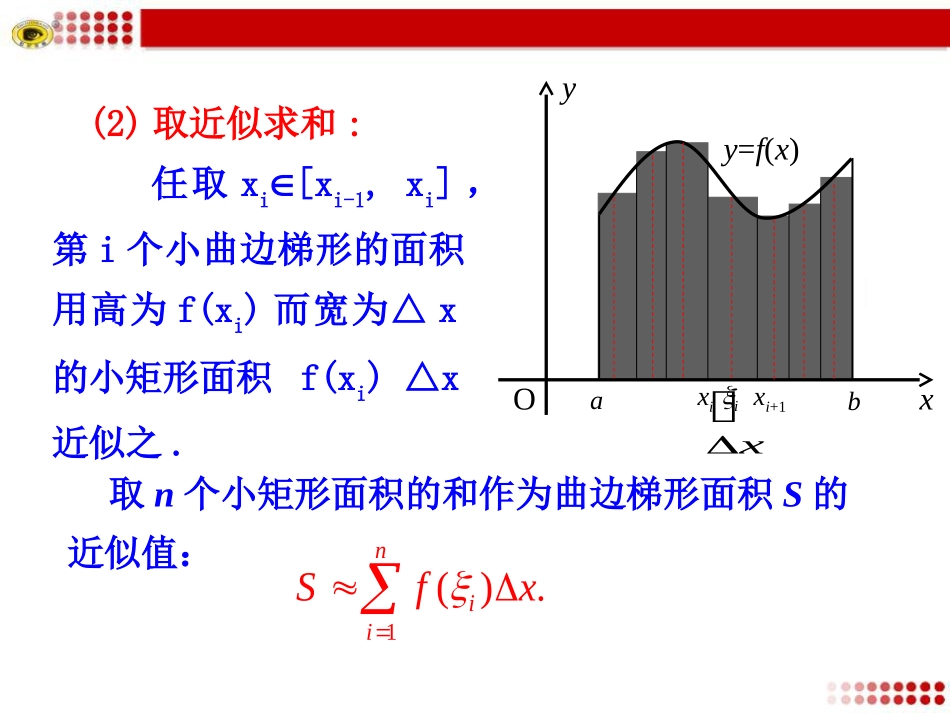
1.5.3定积分的概念求曲线y=f(x)对应的曲边梯形面积的方法xiy=f(x)xyObaxi+1ix(1)分割:在区间[a,b]上等间隔地插入n-1个点,将它等分成n个小区间:每个小区间宽度△x11211,,,,,,,,,iinaxxxxxxb.ban(2)取近似求和:任取xi[xi-1,xi]，第i个小曲边梯形的面积用高为f(xi)而宽为△x的小矩形面积f(xi)△x近似之.xiy=f(x)xyObaxi+1ix取n个小矩形面积的和作为曲边梯形面积S的近似值：1().niiSfx(3)取极限:所求曲边梯形的面积S为xiy=f(x)xyObaxi+1ix1lim().niniSfx1.定积分的计算和简单应用.(重点)2.利用定积分求平面区域围成的面积.(难点)探究点1定积分的定义从求曲边梯形面积S的过程中可以看出,通过以下四步:分割——近似代替——求和——取极限得到解决.0111limlim.nniixniiSfxfn曲边梯形面积11()()nniiiibafxfni-1ii将区间[a,b]等分成n个小区间，在每个小区间[x,x]上任取一点ξ(i=1,2,...,n),作和式011iinaxxxxxb如果函数f(x)在区间[a,b]上连续，用分点定积分的定义0111limlim.nniitniisvtvn变速运动的路程1()lim().nbianibafxdxfn即()[,]()banfxabfxdx当时，上述和式无限接近某个常数，这个常数叫做函数在区间上的定积分，记作[,]())(ababffxdxxx这里，和分别叫做积分下限和积分上限,区间叫做积分区间，函数叫做被积函数，叫做积分变量，叫做被积式.定积分的定义的理解:定积分的相关名称：———叫做积分号，f(x)——叫做被积函数，f(x)dx—叫做被积式，x———叫做积分变量，a———叫做积分下限，b———叫做积分上限，[a,b]—叫做积分区间.Oabxy)(xfy1()lim().nbianibafxdxfn被积函数被积式积分变量积分下限积分上限1()lim().nbianibafxdxfn探究点2定积分()bafxdx的几何意义：如果在区间[a,b]上函数f(x)连续且恒有f(x)≥0,那么定积分()bafxdx表示由直线x=a,x=b,y=0和曲线y=f(x)所围成的曲边梯形的面积.Oxyabyf(x)按定积分的几何意义，有(1)由连续曲线y=f(x)(f(x)0)，直线x=a、x=b及x轴所围成的曲边梯形的面积为(2)设物体运动的速度v=v(t)，则此物体在时间区间[a,b]内运动的距离s为baS=f(x)dx.bas=v(t)dt.1xyOf(x)=x213S根据定积分的定义，右边图形的面积为1120013().Sfxdxxdx同样地，1.5.2中汽车在0≤t≤1这段时间内经过的路程11200523()().svtdttdt(1)定积分是一个数值,它只与被积函数及积分区间有关，而与积分变量的记法无关，即总结提升：()()().bbbaaafxdxftdtfudu(2)定义中区间的分法和i的取法是任意的.3()(()).baabfxdxfxdx()0.baabfxdx特别地，当时，xyO当f(x)0时，由yf(x)、xa、xb与x轴所围成的曲边梯形位于x轴的下方，dxxfSba)]([abyf(x)yf(x)dxxfSba)]([baf(x)dxf(x)dxf(x)dx。Sdxxfba)(().bafxdxS在几何上积分dxxfba)(abyf(x)Oxy()ygx根据定积分的几何意义,如何用定积分表示图中蓝色阴影部分的面积?byf(x)Oxy1()baSfxdx()ygx2()baSgxdx探究点3用定积分表示图中阴影部分的面积12()().bbaaSSSfxdxgxdxa130例1利用定积分的定义,计算xdx的值.3令f（x解）=x：.区间间个点区间个区间···个区间长为(1)分割在0,1上等隔地插入n-1分,i-1i把0,1等分成n小,(i=1,2,,nnii-11n),每小的度Δx=-=.nnn···则in1n0i=1i(2)近似代替、作和取ξ=i=1,2,,n,nifxdxS=fΔxn3ni=1i1=nn2n23244i=111111=i=nn+1=1+.nn44n213n0n→∞n→∞111(3)取极限xdx=limS=lim1+=.4n4探究点4定积分的基本性质性质112[()()]bafxfxdx12()()bbaafxdxfxdx性质2()bakfxdx()bakfxdx(k为常数)性质3.定积分关于积分区间具有可加性1212()()()()bccbaaccfxdxfxdxfxdxfxd...