直线和平面平行的性质定理VIP免费

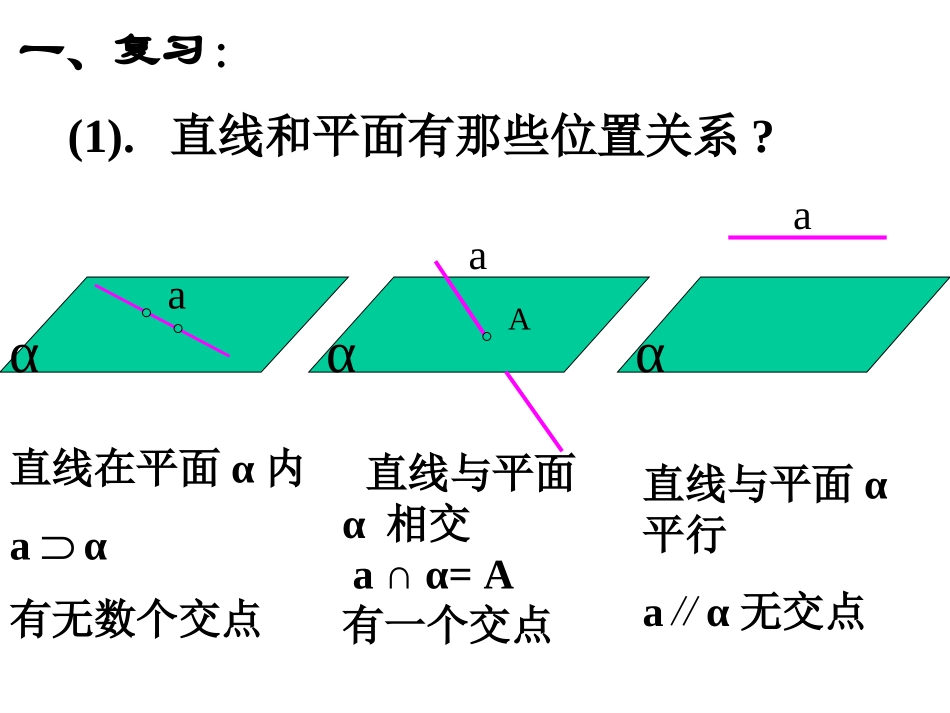
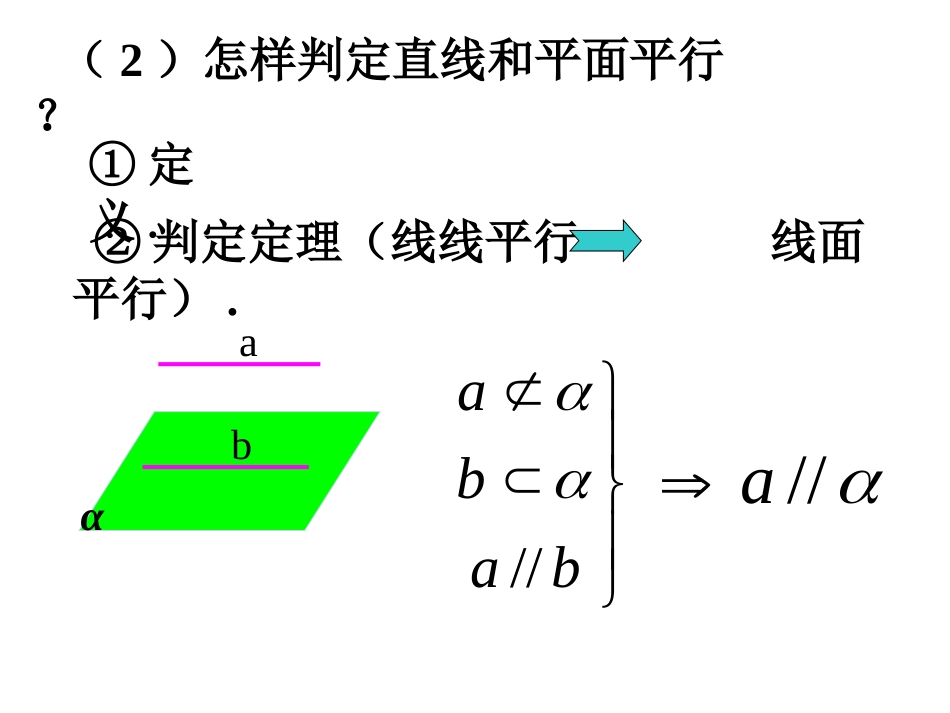
直线和平面平行的性质定理1(1).直线和平面有那些位置关系?αa直线与平面α平行aα∥无交点直线在平面α内aα有无数个交点直线与平面α相交a∩α=A有一个交点αAa一、复习：aα（2）怎样判定直线和平面平行？①定义.//abab②判定定理（线线平行线面平行）.aαb//a（3）如果一条直线和一个平面平行，那么这条直线和这个平面内的直线有怎样的位置关系？abαaαb（4）已知直线a∥平面α，如何在平面α内找出和直线a平行的一条直线？平行异面.交线为所求交，则作一平面与已知平面相过直线a直线和平面平行的性质定理如果一直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行.求证：lm∥证明：∵lα∥∴l和α没有公共点；∴l和m也没有公共点；又l和m都在平面β内，且没有公共点；∴lm.∥αmβ已知：lα,∥lβ,α∩β=m又∵mα二、l(1)“线面平行线线平行”(3)在有线面平行的条件或要证线线平行时，ml∥mll(2)线线平行线面平行babaaα∥证线面平行关键在于找线线平行（中位线、平行四边形）练习:(1).如果一条直线和一个平面平行,这个平面内是否只有一条直线和已知直线平行呢?平面内哪些直线都和已知直线平行?有几条?(有无数条)(不是)(2).如果aα,∥经过a的一组平面分别和α相交于b、c、d…,b、c、d…是一组平行线吗？为什么？(平行，线面平行的性质定理)(3).平行于同一平面的两条直线是否平行？(不一定)(4).过平面外一点与这平面平行的直线有多少条？(无数条)例题讲解：abcαβ证明：过a作平面β交平面α于直线c∵aα∥∴ac∥又∵ab∥∴bc∥∴bα.∥∵bα,cα例1、已知直线a∥直线b，直线a∥平面α,bα求证：b∥平面α例2、求证：如果过平面内一点的直线平行于与此平面平行的一条直线，那么这条直线在此平面内。证明：设l与P确定的平面为β，且α∩β=m'则l∥m',又l∥m，m∩m'=P∴m'和m重合∴mα已知：lα∥，点Pα,P∈∈m且m∥l求证：mα（否则过点P有两条直线与l平行，这与平行公理矛盾）αl．mβm'Plαβ例3、如果两个相交平面分别经过两条平行直线中的一条，那么它们的交线和这两条直线平行.ab∴a∥l同理b∥l又∵aα，平面α∩平面β=l已知:平面α∩平面β=l,aα,bβ,ab∥（如图）求证：a∥l,b∥l.故a∥l,b∥l.证明：∵ab∥，bβ，aβ∴aβ∥例4、有一块木料如图，已知棱BC平行于面A′C′．要经过木料表面A′B′C′D′内的一点P和棱BC将木料锯开，应怎样画线？所画的线和面AC有什么关系？ABCDABCDP练习：（1）直线a∥平面α，平面α内有n条互相平行的直线，那么这n条直线和直线a()（A）全平行（B）全异面（C）全平行或全异面（D）不全平行也不全异面（2）直线a∥平面α，平面α内有无数条直线交于一点，那么这无数条直线中与直线a平行的（）（A）至少有一条（B）至多有一条（C）有且只有一条（D）不可能有CB（1）判定定理和性质定理应用时不要混淆；（2）证线面平行，用判定定理，证线线平行，用性质定理；（3）判定和性质定理同时用来推出线面平行或线线平行，如要证：线线平行，可由判定性质线线平行线面平行线线平行说明：