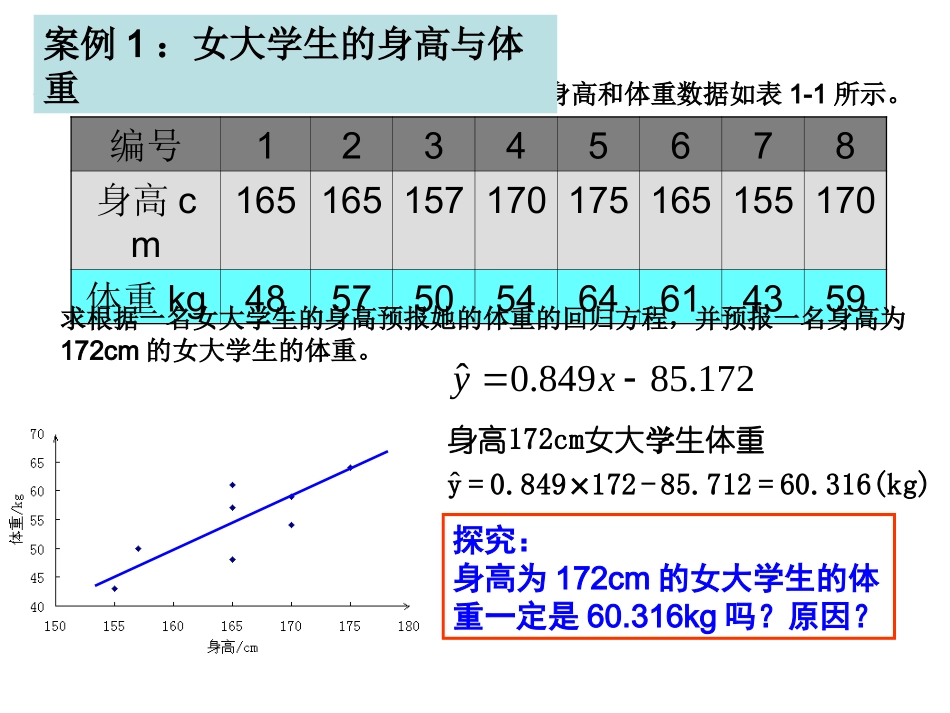
例1从某大学中随机选取8名女大学生,其身高和体重数据如表1-1所示。编号12345678身高cm165165157170175165155170体重kg4857505464614359求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm的女大学生的体重。案例1:女大学生的身高与体重172.85849.0ˆxyˆ学身高172cm女大生体重y=0.849×172-85.712=60.316(kg)探究:身高为172cm的女大学生的体重一定是60.316kg吗?原因?由于所有的样本点不共线,而只是散布在某一直线的附近,所以身高和体重的关系可以用线性回归模型来表示:其中a和b为模型的未知参数,e称为随机误差.eabxy函数模型与回归模型之间的差别一次函数模型:y=bx+a线性回归模型y=bx+a+e增加了随机误差e,因变量y的值由自变量x和随机误差e共同确定,即自变量x只能解析部分y的变化.在统计中,我们也把自变量x称为解释变量,因变量y称为预报变量.线性回归模型:y=bx+a+e函数模型与“回归模型”的关系函数模型:因变量y完全由自变量x确定回归模型:预报变量y完全由解释变量x和随机误差e确定注:e产生的主要原因:(1)所用确定性函数不恰当;(2)忽略了某些因素的影响;(3)观测误差。思考:产生随机误差项e的原因是什么?以上三项误差越小,说明我们的回归模型的拟合效果越好。残差分析在研究两个变量间的时,首先要根据散点图来粗略判断它们是否是线性相关,是否可以用线性回归模型来拟合数据.然后,可以通过残差来判断模型拟合的效果,判断原始数据中是否存在可疑数据.这方面的分析工作称为残差分析.12ˆˆˆ,,,neee0.382-2.8836.6271.137-4.6182.4192.627-6.373残差5943616454505748体重/kg170155165175170157165165身高/cm87654321编号下表为女大学生身高和体重的原始数据以及相应的残差数据:ˆe以纵坐标为残差,横坐标为编号,作出图形(残差图)来分析残差特性.残差图的定义:残差图的制作和作用:制作:坐标纵轴为残差变量,横轴可以有不同的选择.横轴为编号:可以考察残差与编号次序之间的关系,常用于调查数据错误.横轴为解释变量:可以考察残差与解释变量的关系,常用于研究模型是否有改进的余地.作用:判断模型的适用性若模型选择的正确,残差图中的点应该分布在以横轴为中心的带形区域.-8-6-4-2024680246810编号残差系列1异常点•若模型选择的正确,残差图中的点应该分布在以横轴为心的带形区域;•对于远离横轴的点,要特别注意。iiieybxa(1)计算(i=1,2,...n)残差分析(2)画残差图(1)查找异常样本数据(3)分析残差图(2)残差点分布在以O为中心的水平带状区域,并沿水平方向散点的分布规律相同。如何刻画模型拟合的精度?相关指数:22121ˆ()1()niiiniiyyRyyR2取值越大,则残差平方和越小,即模型的拟合效果越好.R2越接近1,表示回归的效果越好(因为R2越接近1,表示解析变量和预报变量的线性相关性越强)。总的来说:相关指数R2是度量模型拟合效果的一种指标。在线性模型中,它代表自变量刻画预报变量的能力。(2)利用R2刻画回归效果R2=1-i=1nyi-y^i2i=1nyi-y2;R2表示______变量对______变量变化的贡献率..解释预报R2=0.64,表明:“女大学生的身高解释了64%的体重变化”,或者说“女大学生的体重差异有64%是由身高引起的”.建立回归模型的基本步骤:(1)确定研究对象,明确哪个变量是解释变量,哪个变量是预报变量;(2)画出确定好的解释变量和预报变量的散点图,观察它们之间的关系(是否存在线性关系);(3)由经验确定回归方程的类型(如观察到数据呈线性关系,则选用线性回归方程y=bx+a);(4)按一定规则估计回归方程中的参数(如最小二乘法);(5)得出结果后分析残差图是否异常(个别数据对应残差过大,或残差呈现不随机的规律性等),若存在异常,则检查数据是否有误,或模型是否合适等.1)确定解释变量和预报变量;2)画出散点图;3)确定回归方程类型;4)求出回归方程;5)利用相关指数或残差进行分析.建立回归模型的基本步骤例1、在一段时间内,某中商品的价格x元和需求量Y件之间的一组数据为:求出Y对的回归直线方...