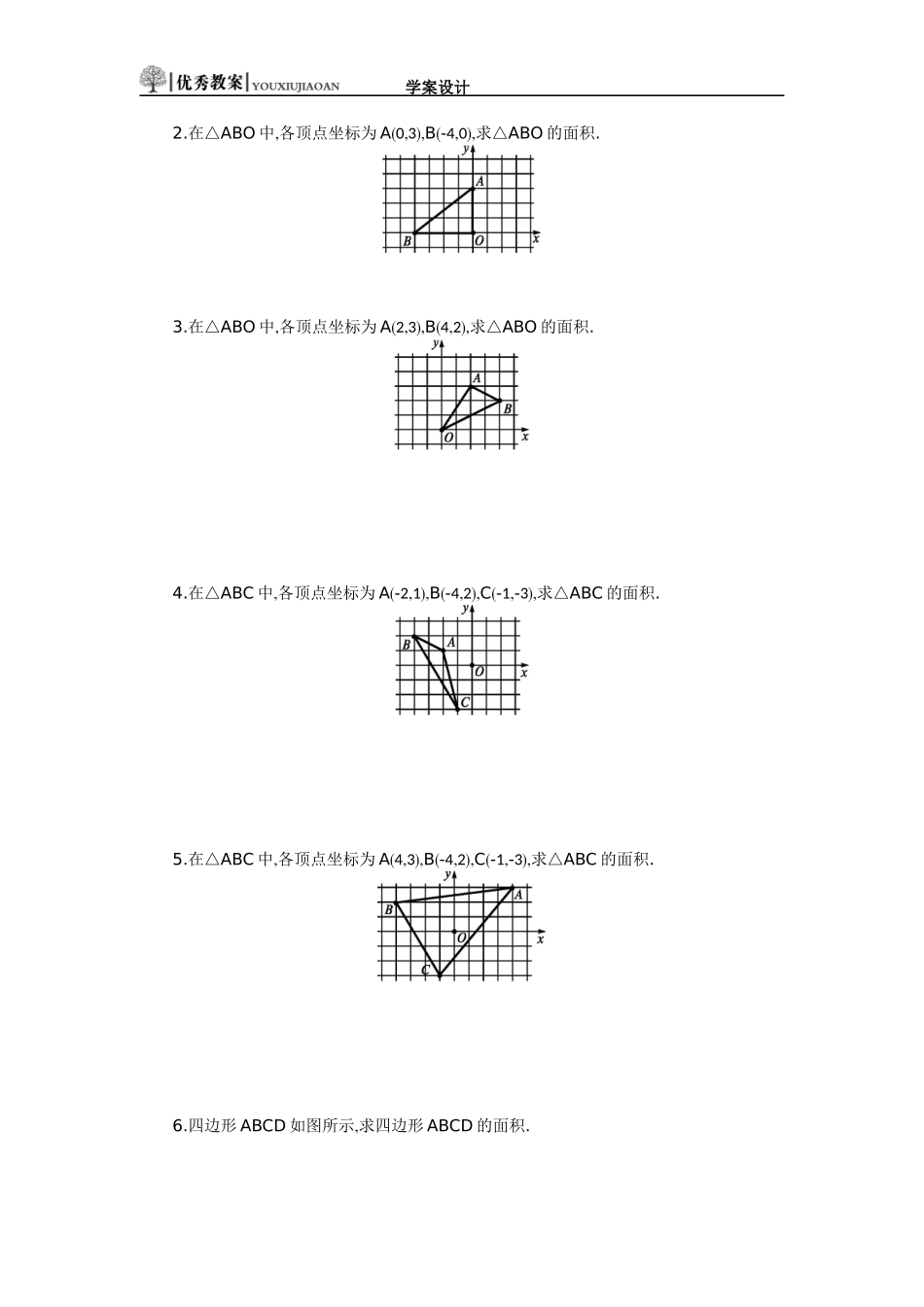
学案设计第七章平面直角坐标系7.2坐标方法的简单应用7.2.2用坐标表示平移(第2课时)学习目标1.进一步认识平面直角坐标系,了解点、图形与坐标的对应关系;能求出给定坐标的点构成的图形的面积.2.能建立适当的平面直角坐标系,通过描点连线,求解图形面积,进一步体会平面直角坐标系在实际生活中的作用.自主学习问题:如图,在△ABC中,任意一点P(x,y)经平移后对应点为P'(x+4,y+3),将△ABC作同样的平移得到△A'B'C',求点A',B',C'的坐标.合作探究一【例题】如图,在△ABC中,各顶点坐标为A(0,3),B(-1,0),C(3,0),求△ABC的面积.合作探究二1.在△ABC中,各顶点坐标为A(0,3),B(-1,0),C(-5,0),求△ABC的面积.学案设计2.在△ABO中,各顶点坐标为A(0,3),B(-4,0),求△ABO的面积.3.在△ABO中,各顶点坐标为A(2,3),B(4,2),求△ABO的面积.4.在△ABC中,各顶点坐标为A(-2,1),B(-4,2),C(-1,-3),求△ABC的面积.5.在△ABC中,各顶点坐标为A(4,3),B(-4,2),C(-1,-3),求△ABC的面积.6.四边形ABCD如图所示,求四边形ABCD的面积.学案设计课堂练习1.如图,在直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).(1)写出点A,B的坐标:A,B.(2)△ABC的面积为平方单位.(3)将△ABC先向左平移3个单位长度,再向上平移2个单位长度,得到△A'B'C',则△A'B'C'的三个顶点坐标分别是A',B',C'.2.在平面直角坐标系中,已知点A(-4,3),B(-2,-3).(1)描出A,B两点的位置,并连接AB,AO,BO.(2)△AOB的面积是.(3)把△AOB向右平移4个单位长度,再向上平移2个单位长度,画出平移后的△A'B'C',并写出各顶点的坐标.3.如图,在直角坐标系中,△ABC的顶点都在网格点上.(1)平移△ABC,使点C与坐标原点O是对应点,请画出平移后的三角形△A1B1O,并写出A,B两点的对应点A1,B1的坐标;(2)求△ABC的面积.学案设计参考答案自主学习合作探究一【例题】解:根据图形可知AO⊥BC,由△ABC的顶点坐标可知AO=3,BC=4,S△ABC=12AO·BC=12×3×4=6.合作探究二1.解:根据图形可知AO⊥BC,由△ABC的顶点坐标可知AO=3,BC=4S△ABC=12AO·BC=12×3×4=6.2.解:根据图形可知AO⊥BO,由△ABO的顶点坐标可知AO=3,BO=4S△ABO=12AO·BO=12×3×4=6.3.解:S△ABO=3×4-12×2×4-12×3×2-12×2×1=4.4.解:S△ABC=3×5-12×2×1-12×3×5-12-12×1×4=3.5.5.解:S△ABC=6×8-12×1×8-12×3×5-12×5×6=21.5.6.解:S△ABC=5×6-12×1×6-12×2×4-12×4×1-12×5×1=18.5.课堂练习1.(1)(2,-1)(4,3)(2)5(3)(-1,1)(1,5)(-2,4)2.(1)图略(2)9(3)图略A'(0,5),B'(2,-1),C'(4,2)3.(1)图略A'(1,-3),B'(3,1)(2)5