竞赛课件7：曲线运动曲直谈VIP免费

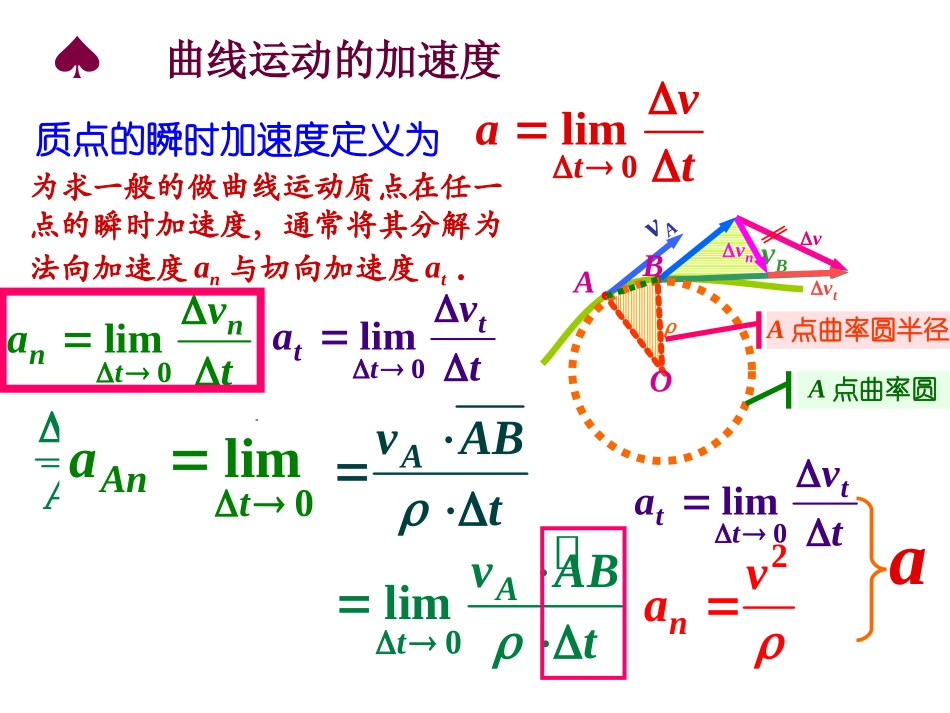
一、曲线运动的发生条件F合外力方向与速度方向不在一直线二、曲线运动的特点速度方向一定变化切向力改变速度大小法向力改变速度方向vFnFt三、求解曲线运动问题的运动学基本方法矢量的合成与分解微元法曲线运动的加速度♠质点的瞬时加速度定义为0limtvatAvAvBvnvtv0limnntvat0limtttvat为求一般的做曲线运动质点在任一点的瞬时加速度，通常将其分解为法向加速度an与切向加速度at．OA点曲率圆nAvvABnAvvABtt0limAnta0limAtvABt2nvaA点曲率圆半径0limtttvataB在离水面高度为h的岸边，有人用绳子拉船靠岸，若人收绳的速率恒为v0，试求船在离岸边s距离处时的速度与加速度的大小各为多少？专题专题7-7-例例11依据实际运动效果分解船的运动：v0Avvnhsvt船及与船相系的绳端A的实际运动是水平向左的，这可看作是绳之A端一方面沿绳方向向“前方”滑轮处“收短”，同时以滑轮为圆心转动而成，即将实际速度v分解成沿绳方向“收短”的分速度vn和垂直于绳方向的转动分速度vt;注意到绳子是不可伸长的，人收绳的速率v0也就是绳端A点沿绳方向移动速率vn:由图示v、vt、vn矢量关系及位置的几何关系易得：0nvv00cotthvvvs0sinvv则220hsvs求船的速度续解求船的加速度在一小段时间Δt内,船头位置从A移A′，绳绕滑轮转过一小角度Δθ→0:Avv0vtAvv0tv0sinvv读题011sinsinvv由加速度定义得：0limtvat0costancosthhtvv由几何关系得：cosh00011sinsinlimtancosvahv则200sinsincoslimtansinsinvh200cossincos22limtansinsin2vh230cotvh2203vhs320vhhs质点沿圆周做速度大小、方向均变化的运动．每个瞬时的加速度均可分解为切向加速度at与法向加速度an，前者反映质点速率变化快慢，后者反映质点速度方向变化快慢．如图所示，质点从O点由静止开始沿半径为R的圆周做速率均匀增大的运动，到达A点时质点的加速度与速度方向夹角为α，质点通过的弧s所对的圆心角为β，试确定α与β间的关系．专题专题7-7-例例22vAaAOβsatan由题给条件22tnataR则222,AntaasvRt而22,AtvatsR2nttaataR222sttR2tanntaa又tan2如图所示，质点沿一圆周运动，过M点时速度大小为v，作加速度矢量与圆相交成弦MA=l，试求此加速度的大小．将M点加速度沿切向与法向进行分解!vaMAlOatan法向加速度2sinnvaaR22avlsin=2而lR2sinvaR如图所示，曲柄OA长40cm,以等角速度ω=0.5rad/s绕O轴反时针方向转动．由于曲柄的A端推动水平板B而使滑杆C沿竖直方向上升，求当曲柄与水平线夹角θ=30°时，滑杆C的加速度．杆A与B板接触点有相同沿竖直方向的加速度!杆上A点加速度2AalOABCωθaAaAyaC20.05m/sBa21sin2AyAaalθ此即滑杆C的加速度CAyaa代入数据得滑杆C的加速度有一只狐狸以不变的速度v1沿着直线AB逃跑，一猎犬以不变的速率v2追击，其运动方向始终对准狐狸．某时刻狐狸在F处，猎犬在D处，FD⊥AB，且FD＝L，如图．试求此时猎犬的加速度的大小．设Δt时间内，v2方向变化Δθ,Δθ→0时:FLABDABv1v2v2vv21vtv21tanvtL由加速度定义，猎犬加速度0limtvat20limtvt12avvL赛车在公路的平直段上以尽可能大的加速度行驶，在0.1s内速度由10.0m／s加大到10.5m／s，那么该赛车在半径为30m的环形公路段行驶中，要达到同样大的速度需要多少时间？当环形公路段的半径为多少时，赛车的速度就不可能增大到超过10m/s？（公路的路面是水平的）直线加速时车的加速度:20005m/stvvat在环形公路上，法向加速度2tnvaR0ttvvat切向加速度2220ntaaa代入数据4210.50.25...