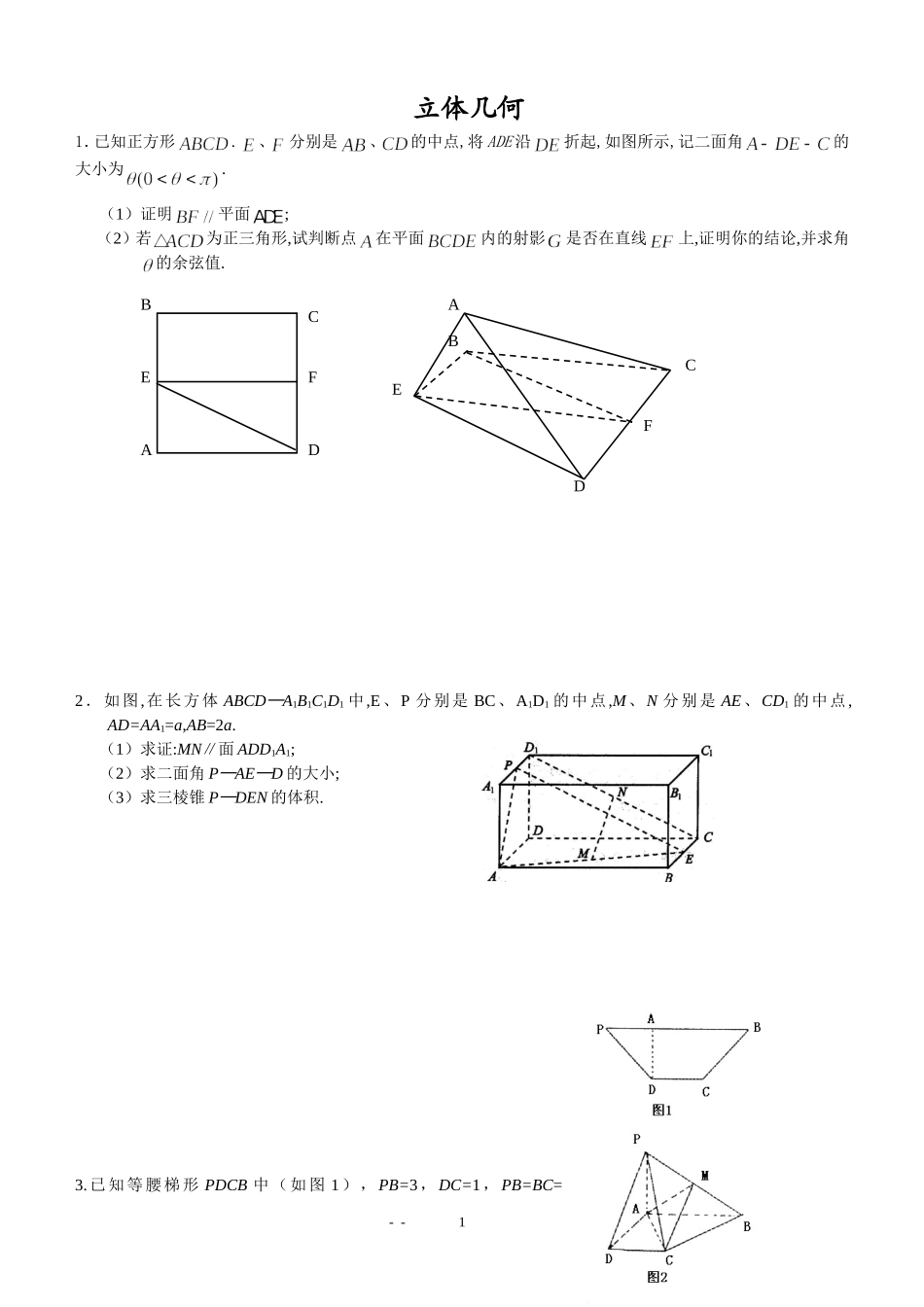
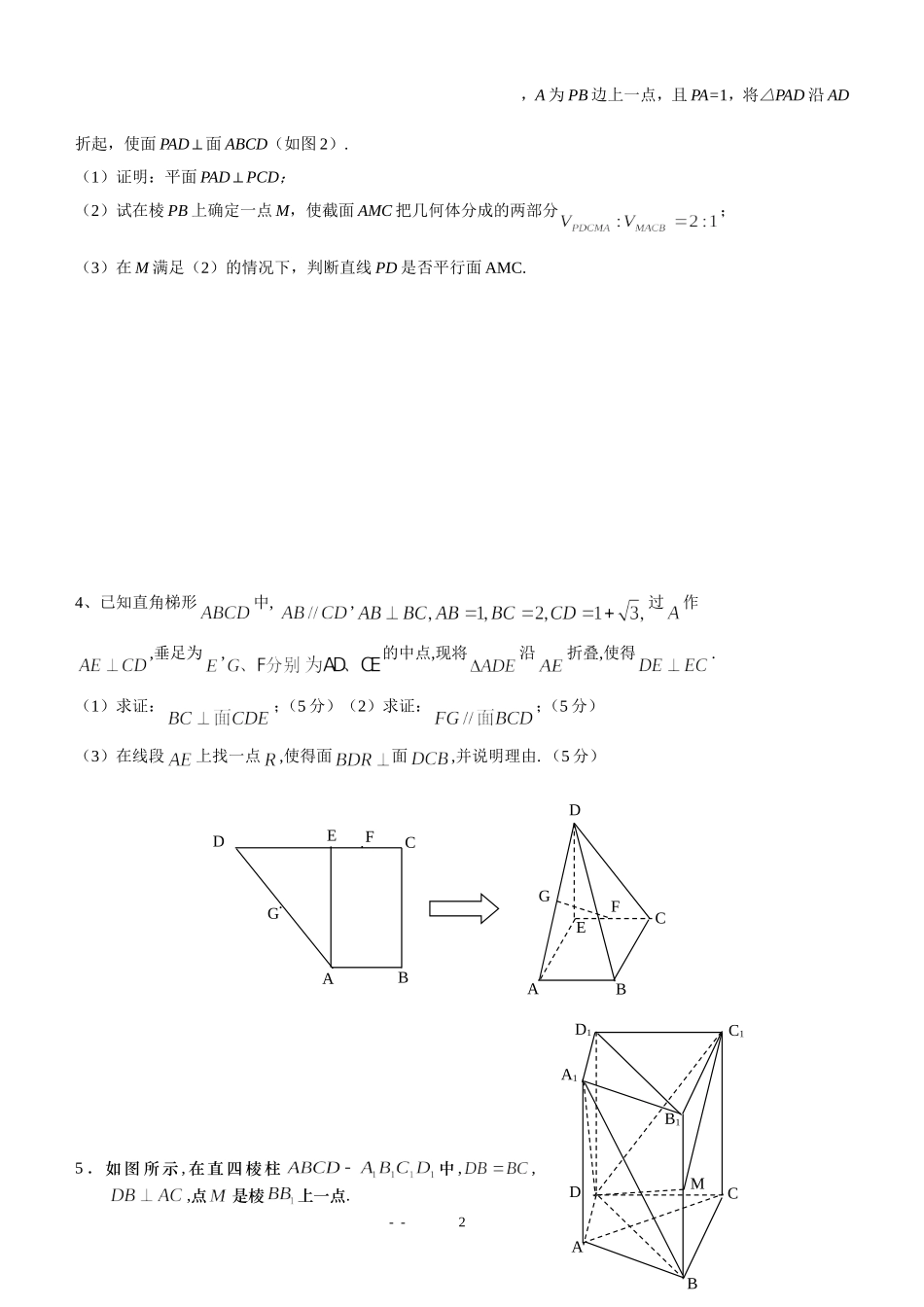
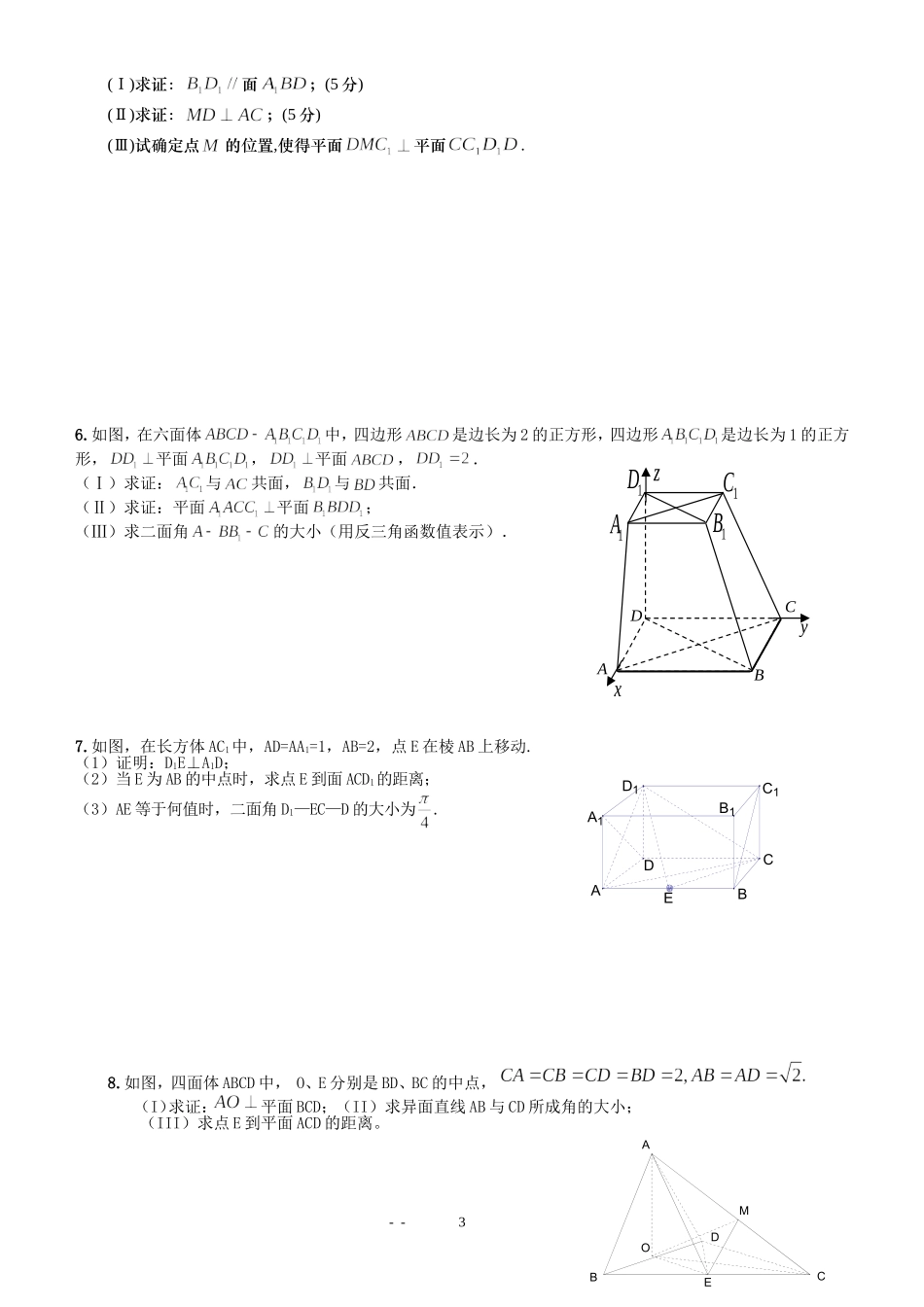
立体几何1.已知正方形.、分别是、的中点,将ADE沿折起,如图所示,记二面角的大小为.(1)证明平面;(2)若为正三角形,试判断点在平面内的射影是否在直线上,证明你的结论,并求角的余弦值.2.如图,在长方体ABCD─A1B1C1D1中,E、P分别是BC、A1D1的中点,M、N分别是AE、CD1的中点,AD=AA1=a,AB=2a.(1)求证:MN∥面ADD1A1;(2)求二面角P─AE─D的大小;(3)求三棱锥P─DEN的体积.3.已知等腰梯形PDCB中(如图1),PB=3,DC=1,PB=BC=--AACBDEFBCDEF1,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD(如图2).(1)证明:平面PAD⊥PCD;(2)试在棱PB上确定一点M,使截面AMC把几何体分成的两部分;(3)在M满足(2)的情况下,判断直线PD是否平行面AMC.4、已知直角梯形中,,过作,垂足为,的中点,现将沿折叠,使得.(1)求证:;(5分)(2)求证:;(5分)(3)在线段上找一点,使得面面,并说明理由.(5分)5.如图所示,在直四棱柱中,,,点是棱上一点.--2ABCDEGF··ABCDEGFMABCDA1B1C1D1D1C1B1A1EDCBA(Ⅰ)求证:面;(5分)(Ⅱ)求证:;(5分)(Ⅲ)试确定点的位置,使得平面平面.6.如图,在六面体中,四边形是边长为2的正方形,四边形是边长为1的正方形,平面,平面,.(Ⅰ)求证:与共面,与共面.(Ⅱ)求证:平面平面;(Ⅲ)求二面角的大小(用反三角函数值表示).7.如图,在长方体AC1中,AD=AA1=1,AB=2,点E在棱AB上移动.(1)证明:D1E⊥A1D;(2)当E为AB的中点时,求点E到面ACD1的距离;(3)AE等于何值时,二面角D1—EC—D的大小为.8.如图,四面体ABCD中,O、E分别是BD、BC的中点,(I)求证:平面BCD;(II)求异面直线AB与CD所成角的大小;(III)求点E到平面ACD的距离。--3ABMDEOCABCD1A1B1C1Dxyz9.如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是地面边长的2倍,P为侧棱SD上的点。(Ⅰ)求证:AC⊥SD;(Ⅱ)若SD⊥平面PAC,求二面角P-AC-D的大小(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC。若存在,求SE:EC的值;若不存在,试说明理由。10如图,在三棱锥PABC中,PA底面,,60,90ABCPAABABCBCA,点D,E分别在棱,PBPC上,且//DEBC(Ⅰ)求证:BC平面PAC;(Ⅱ)当D为PB的中点时,求AD与平面PAC所成的角的大小;(Ⅲ)是否存在点E使得二面角ADEP为直二面角?并说明理由.--4