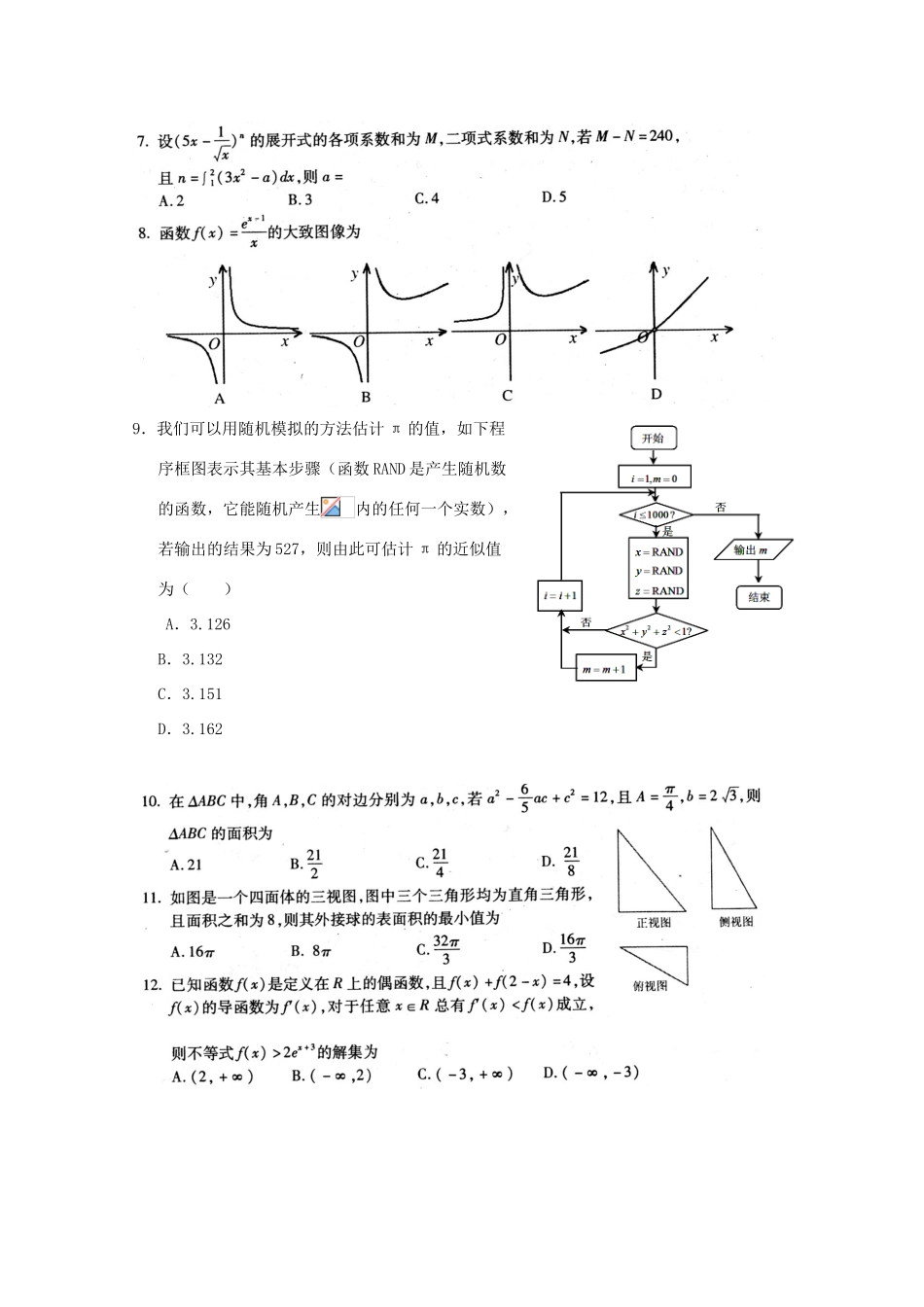
2017年高考仿真模拟考试(三)数学(理科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.5.已知某批零件的长度误差(单位:毫米)服从正态分布,从中随机取一件,其长度误差落在区间内的概率为(附:若随机变量服从正态分布,,则A.4.56%B.13.59%C.27.18%D.31.74%9.我们可以用随机模拟的方法估计π的值,如下程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生内的任何一个实数),若输出的结果为527,则由此可估计π的近似值为()A.3.126B.3.132C.3.151D.3.16218、(本题满分12分)2017年春节期间,某服装超市举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸到2个红球,则打6折,若摸到1个红球,则打7折;若没有摸到红球,则不打折.方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回摸取,连摸3次,每摸到一个红球,立减200元。(1)若两位顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;(2)若某顾客恰好消费了1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?参考答案一、选择题:DBACBABBDCAD二、填空题:13.14.15.16.三、解答题:17.解:(Ⅰ)当时,,∴…………1分当时,……………3分显然对也成立,……………4分∴的通项公式为()…………5分(Ⅱ)当时,,;……………6分当时,,;……………7分当时,,且为递增数列,∴当时,.……………8分∴当时,。…11分综上,……………12分19.解:(Ⅰ)证明:因为均垂直于平面,所以,……………1分又由于,,故有所以,从而,……3分18、、所以四点共面.……………4分另证:分别过点作交于点、过点作交于点,连接,易证且,所以,即四点共面.(Ⅱ)如图,以所在直线分别为轴建立空间直角坐标系,…………5分不妨设,则,则,,……………7分设平面的一个法向量为,由得,令,则,……9分……………11分故所求正弦值为……………12分20.解:(Ⅰ)①曲线为直线;………………………………………1分②时,曲线为焦点在轴上的椭圆;…………2分③当,曲线为焦点在轴上的双曲线.……3分(Ⅱ)当时,曲线的方程为.………………………………4分设,则A,B的坐标满足消去y化简得由得……………………5分∴,,………………………………6分∴=.………………7分,,即∴即………………………8分=.……………………………9分点到直线的距离,…………………10分∴===为定值.………12分21.解:(Ⅰ)………1分∵,∴,∴在单调递减,在单调递增.…(Ⅱ)当时,若,则,不合题意.(或:当时,0—,而,所以,不合题意.)∴当对任意的恒成立时,.………4分由(1)知,当时,在单调递减,在单调递增.则.………6分,()…7分设,则,∴在上单调递增.又,.………8分∴存在唯一,使得.………9分当时,,则,∴在上单调递增.当时,,则,∴在上单调递减.∴()………10分设,.∵,∴,∴.………11分∴在单调递减,故的值域为,∴函数的最大值的取值范围为,…………12分22.解:(Ⅰ)直线的极坐标方程为……2分由的参数方程得……3分圆的极坐标方程:……5分(Ⅱ),代入得,……6分,代入得,…7分∴…8分∵,∴,且为减函数,∴综上:的取值范围为。……10分23、解:(Ⅰ)由题可知:成立成立,,…………2分∴.①当时,,.…………3分②当时,,,不成立,舍去.…………4分③当时,,,或.…………5分(Ⅱ)∵,…………8分∴.又∵不等式的解集不是空集,∴.…………10分