高考数学基础知识梳理：集合与简易逻辑 新人教A版VIP免费

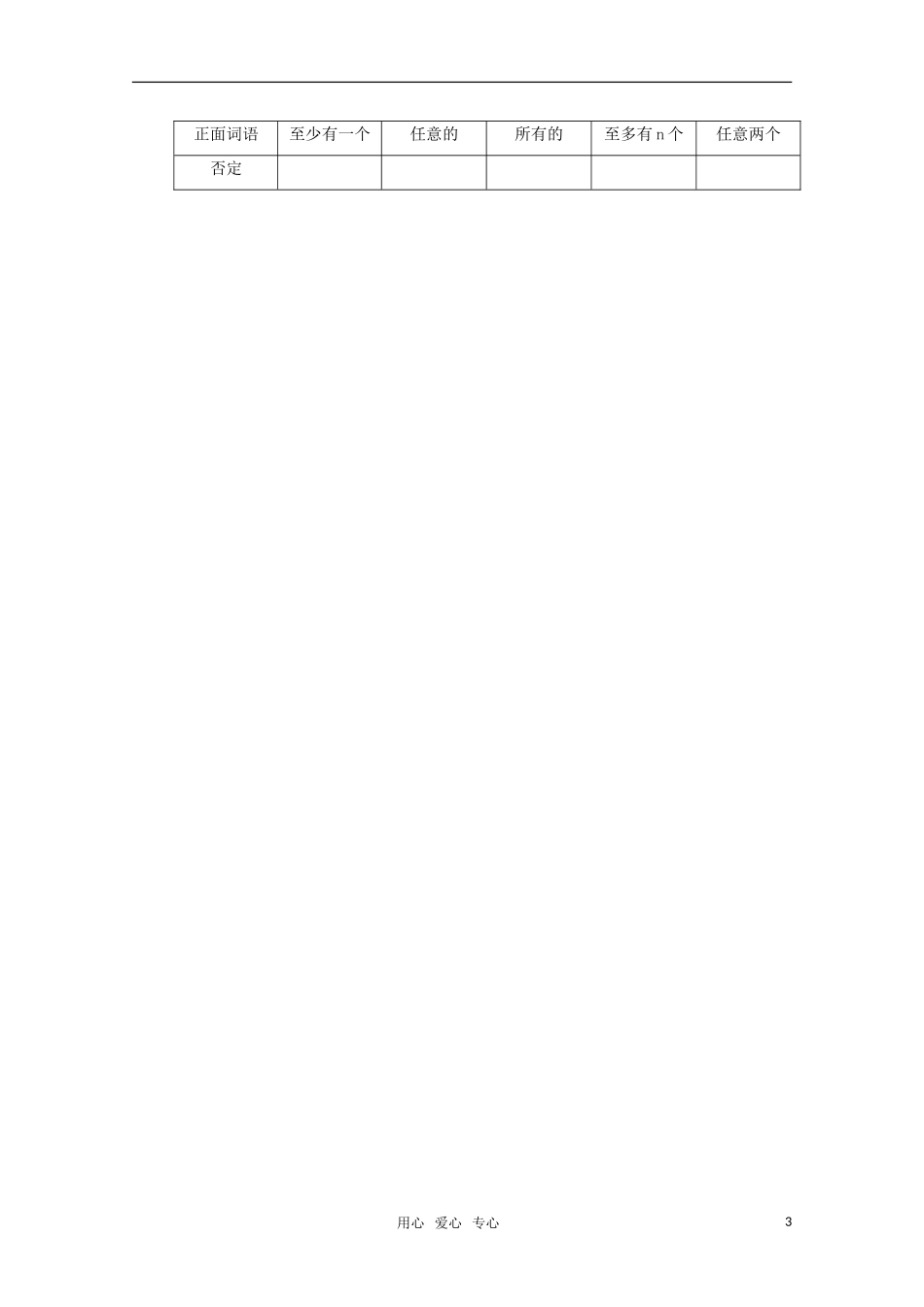
高考数学基础知识、常见结论详解一、集合与简易逻辑一、理解集合中的有关概念（1）集合中元素的特征：确定性，互异性，无序性。集合元素的互异性：如：)}lg(,,{xyxyxA，}|,|,0{yxB，求A；（2）集合与元素的关系用符号，表示。（3）常用数集的符号表示：自然数集；正整数集、；整数集；有理数集、实数集。（4）集合的表示法：列举法，描述法，韦恩图。注意：区分集合中元素的形式：如：}12|{2xxyxA；}12|{2xxyyB；}12|),{(2xxyyxC；}12|{2xxxxD；},,12|),{(2ZyZxxxyyxE；}12|)',{(2xxyyxF；},12|{2xyzxxyzG（5）空集是指不含任何元素的集合。（}0{、和}{的区别；0与三者间的关系）空集是任何集合的子集，是任何非空集合的真子集。注意：条件为BA，在讨论的时候不要遗忘了A的情况。如：}012|{2xaxxA，如果RA，求a的取值。二、集合间的关系及其运算（1）符号“,”是表示元素与集合之间关系的，立体几何中的体现点与直线（面）的关系；符号“,”是表示集合与集合之间关系的，立体几何中的体现面与直线(面)的关系。（2）_}__________{_________BA；____}__________{_________BA；_}__________{_________ACU（3）对于任意集合BA,，则：①ABBA___；ABBA___；BABA___；②ABA；ABA；用心爱心专心1UBACU；BACU；③BCACUU；)(BACU；（4）①若n为偶数，则n；若n为奇数，则n；②若n被3除余0，则n；若n被3除余1，则n；若n被3除余2，则n；三、集合中元素的个数的计算：（1）若集合A中有n个元素，则集合A的所有不同的子集个数为_________，所有真子集的个数是__________，所有非空真子集的个数是。（2）BA中元素的个数的计算公式为：)(BACard；（3）韦恩图的运用：四、xxA|{满足条件}p，xxB|{满足条件}q，若；则p是q的充分非必要条件BA_____；若；则p是q的必要非充分条件BA_____；若；则p是q的充要条件BA_____；若；则p是q的既非充分又非必要条件___________；五、原命题与逆否命题，否命题与逆命题具有相同的；注意：“若qp，则qp”在解题中的运用，如：“sinsin”是“”的条件。六、反证法：当证明“若p，则q”感到困难时，改证它的等价命题“若q则p”成立，步骤：1、假设结论反面成立；2、从这个假设出发，推理论证，得出矛盾；3、由矛盾判断假设不成立，从而肯定结论正确。矛盾的来源：1、与原命题的条件矛盾；2、导出与假设相矛盾的命题；3、导出一个恒假命题。适用与待证命题的结论涉及“不可能”、“不是”、“至少”、“至多”、“唯一”等字眼时。正面词语等于大于小于是都是至多有一个否定用心爱心专心2正面词语至少有一个任意的所有的至多有n个任意两个否定用心爱心专心3