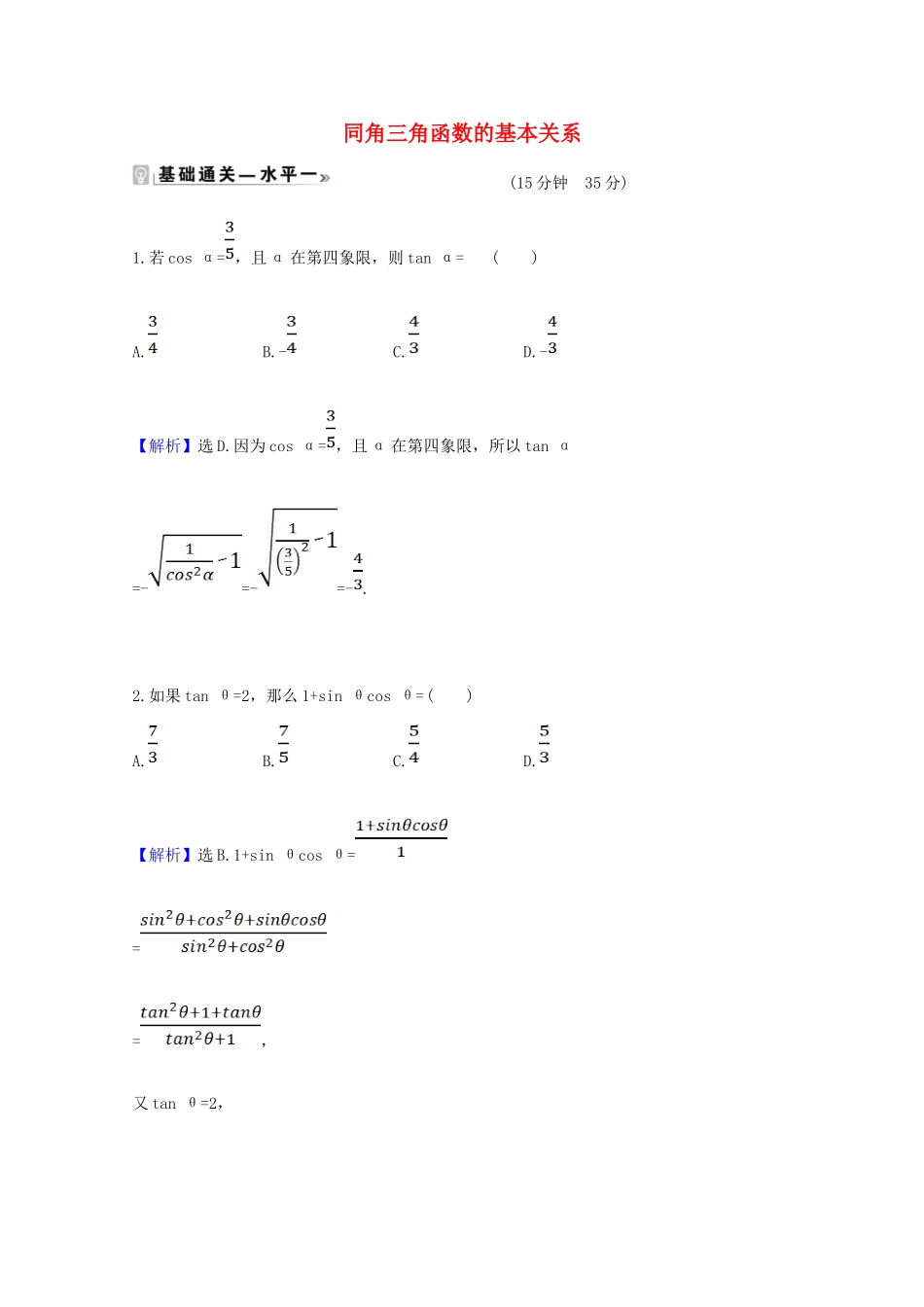
同角三角函数的基本关系(15分钟35分)1.若cosα=,且α在第四象限,则tanα=()A.B.-C.D.-【解析】选D.因为cosα=,且α在第四象限,所以tanα=-=-=-.2.如果tanθ=2,那么1+sinθcosθ=()A.B.C.D.【解析】选B.1+sinθcosθ===,又tanθ=2,所以1+sinθcosθ==.3.已知sinα=,则sin4α-cos4α的值为()A.-B.-C.D.【解析】选A.sin4α-cos4α=(sin2α+cos2α)(sin2α-cos2α)=sin2α-(1-sin2α)=2sin2α-1=2×-1=-.4.若α为第三象限角,则+的值为()A.3B.-3C.1D.-1【解析】选B.因为α为第三象限角,所以原式=+=-3.5.已知tanθ=2,则+sin2θ的值为_______.【解析】因为tanθ=2,所以+sin2θ=+=+=+=.答案:6.化简:(1);(2).【解析】(1)原式=====1.(2)原式===cosθ.(30分钟60分)一、单选题(每小题5分,共20分)1.若α∈,sinα=,则tanα=()A.-B.-C.-D.【解析】选C.因为α∈,且sinα=,所以cosα=-=-,则tanα===-.2.已知=2,则tan2α-3tanα=()A.2B.0C.-D.-【解析】选C.==2,解得tanα=,所以tan2α-3tanα=-3×=-.3.已知α为第二象限的角,且tanα=-,则sinα+cosα=()A.-B.-C.-D.【解析】选C.tanα==-①,sin2α+cos2α=1②,又α为第二象限的角,所以sinα>0,cosα<0,联立①②,解得sinα=,cosα=-,则sinα+cosα=-.【补偿训练】若△ABC的内角A满足sinA·cosA=,则sinA+cosA的值为()A.B.-C.D.-【解析】选A.因为A为△ABC的内角,且sinAcosA=>0,所以A为锐角,所以sinA+cosA>0.又1+2sinAcosA=1+=,即(sinA+cosA)2=,所以sinA+cosA=.4.若α是三角形的最大内角,且sinα-cosα=,则三角形是()A.钝角三角形B.锐角三角形C.直角三角形D.等腰三角形【解析】选B.将sinα-cosα=两边平方,得1-2sinαcosα=,即2sinαcosα=.又α是三角形的内角,所以sinα>0,cosα>0,所以α为锐角.【误区警示】根据sinα·cosα>0判断sinα,cosα的正负时,注意不要忘了条件α是三角形最大的内角.二、多选题(每小题5分,共10分,全部选对得5分,选对但不全的得3分,有选错的得0分)5.下列选项可能成立的是()A.sinα=-且cosα=B.sinα=0且cosα=-1C.tanα=1且cosα=-1D.tanα=(α在第二象限)【解析】选A、B、D.由基本关系式可逐个判断A、B、D正确,C不正确.6.若1+sinθ+cosθ=0成立,则θ不可能位于()A.第一象限B.第二象限C.第三象限D.第四象限【解析】选A、B、D.因为1+sinθ+cosθ·=0,所以1+sinθ|sinθ|+cosθ|cosθ|=0.当θ为第一象限角时,1+sin2θ+cos2θ=2;当θ为第二象限角时,1+sin2θ-cos2θ=2sin2θ>0;当θ为第三象限角时,1-sin2θ-cos2θ=1-1=0;当θ为第四象限角时,1-sin2θ+cos2θ=2cos2θ>0,则θ不可能是第一、二、四象限角.【光速解题】在第一、二、三、四象限内分别取一个特殊角,代入验证,即可得到答案.三、填空题(每小题5分,共10分)7.(2020·青岛高一检测)若sinθ+cosθ=(0≤θ≤π),则tanθ=_______.【解题指南】把已知等式两边平方,可得2sinθcosθ=-,求出sinθ-cosθ的值,从而求出sinθ,cosθ的值,则tanθ可求.【解析】由sinθ+cosθ=,两边平方得:sin2θ+cos2θ+2sinθcosθ=,则2sinθcosθ=-,又因为θ∈[0,π],所以sinθ>0,cosθ<0,则sinθ-cosθ===.所以sinθ=,cosθ=-,则tanθ==-.答案:-【补偿训练】若cosθ+sinθ=,θ∈(0,π),则cosθsinθ-sin2θ=_______.【解析】因为cosθ+sinθ=,①所以两边平方可得:1+2sinθcosθ=,解得2sinθcosθ=-,因为θ∈(0,π),sinθ>0,可得cosθ<0,所以cosθ-sinθ<0,所以cosθ-sinθ=-=-=-=-,②所以联立①②解得:sinθ=,cosθ=-,所以cosθsinθ-sin2θ=sinθ(cosθ-sinθ)=-.答案:-8.在△ABC中,若tanA=,则sinA=_______,cosA=_______.【解析】由tanA=>0且角A是△ABC的内角,可得0