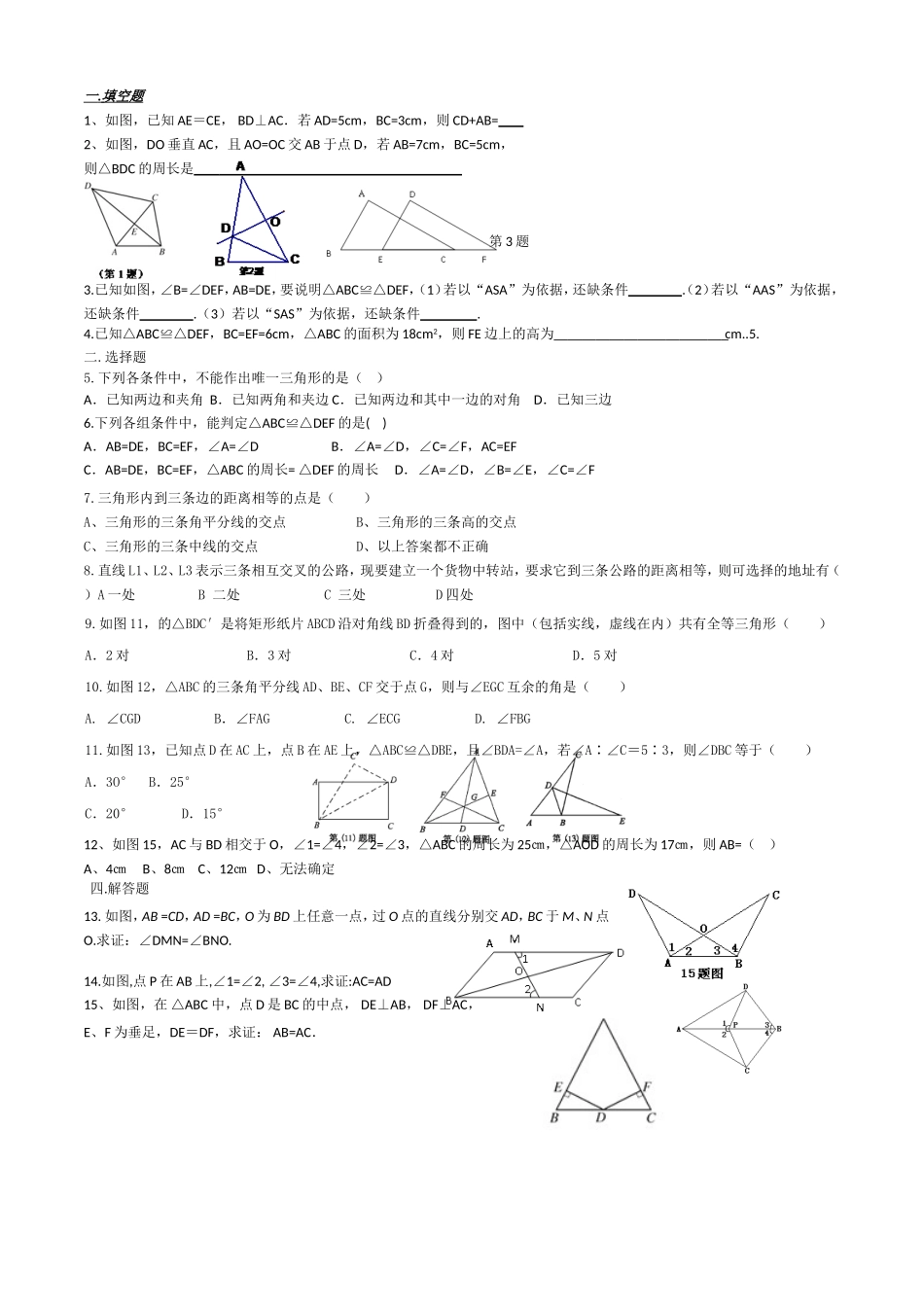
八年级数学上册期末复习学案第十一章全等三角形一、知识要点1、能够____________的两个三角形叫做全等三角形,把两个全等的三角形重合到一起,重合的顶点叫____________,重合的边叫_________,重合的角叫_________.2、平移、翻折、旋转前后的两个图形_____________.3、全等三角形的性质:(1)全等三角形的________________相等;(2)全等三角形的________________相等;(3)全等三角形的________________相等;(4)全等三角形的________________相等;4、全等三角形的判定方法:____________________________________________________.5、角平分线的性质定理:______________________________________________________.逆定理:___________________________________________________________________.二、例题:1.已知如图(1),≌,其中的对应边:____与____,____与____,____与____,对应角:______与_______,______与_______,______与_____2.如图(2),≌,BC的延长线交DA于F,交DE于G,,,求、的度数.3.如图(3),在中,,D、E分别为AC、AB上的点,且AD=BD,AE=BC,DE=DC.求证:DE⊥AB。(图3)4.如图(4),AB=AC,BE和CD相交于P,PB=PC,求证:PD=PE.(4)5、如图(5),在中,M在BC上,D在AM上,AB=AC,DB=DC。求证:MB=MC(5)6、.如图(6),AD与BC相交于O,OC=OD,OA=OB,求证:(6)7、如图(7),在中,AB=AC,D、E分别在BC、AC边上。且,AD=DE求证:≌.8、如图(8),在中,,沿过点A的一条直线AD折叠,使点C恰好落在AB变的中点E处,则∠A的度数=。9、如图(9),在中,平分,那么点到直线的距离是_(8)(9)10、如图(10),已知在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D.(1)若∠BAC=30°,则AD与BD之间有何数量关系,说明你的理由;(2)若AP平分∠BAC,交BD于P,求∠BPA的度数.三、练习题PABCDE一.填空题1、如图,已知AE=CE,BD⊥AC.若AD=5cm,BC=3cm,则CD+AB=2、如图,DO垂直AC,且AO=OC交AB于点D,若AB=7cm,BC=5cm,则△BDC的周长是第3题3.已知如图,∠B=∠DEF,AB=DE,要说明△ABC≌△DEF,(1)若以“ASA”为依据,还缺条件.(2)若以“AAS”为依据,还缺条件.(3)若以“SAS”为依据,还缺条件.4.已知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为18cm2,则FE边上的高为cm..5.二.选择题5.下列各条件中,不能作出唯一三角形的是()A.已知两边和夹角B.已知两角和夹边C.已知两边和其中一边的对角D.已知三边6.下列各组条件中,能判定△ABC≌△DEF的是()A.AB=DE,BC=EF,∠A=∠DB.∠A=∠D,∠C=∠F,AC=EFC.AB=DE,BC=EF,△ABC的周长=△DEF的周长D.∠A=∠D,∠B=∠E,∠C=∠F7.三角形内到三条边的距离相等的点是()A、三角形的三条角平分线的交点B、三角形的三条高的交点C、三角形的三条中线的交点D、以上答案都不正确8.直线L1、L2、L3表示三条相互交叉的公路,现要建立一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有()A一处B二处C三处D四处9.如图11,的△BDC′是将矩形纸片ABCD沿对角线BD折叠得到的,图中(包括实线,虚线在内)共有全等三角形()A.2对B.3对C.4对D.5对10.如图12,△ABC的三条角平分线AD、BE、CF交于点G,则与∠EGC互余的角是()A.∠CGDB.∠FAGC.∠ECGD.∠FBG11.如图13,已知点D在AC上,点B在AE上,△ABC≌△DBE,且∠BDA=∠A,若∠A∶∠C=5∶3,则∠DBC等于()A.3O°B.25°C.20°D.15°12、如图15,AC与BD相交于O,∠1=∠4,∠2=∠3,△ABC的周长为25㎝,△AOD的周长为17㎝,则AB=()A、4㎝B、8㎝C、12㎝D、无法确定四.解答题13.如图,AB=CD,AD=BC,O为BD上任意一点,过O点的直线分别交AD,BC于M、N点O.求证:∠DMN=∠BNO.14.如图,点P在AB上,∠1=∠2,∠3=∠4,求证:AC=AD15、如图,在△ABC中,点D是BC的中点,DE⊥AB,DF⊥AC,E、F为垂足,DE=DF,求证:AB=AC.