2012新课标高考数学热点集中营热点12函数性质的综合应用VIP免费

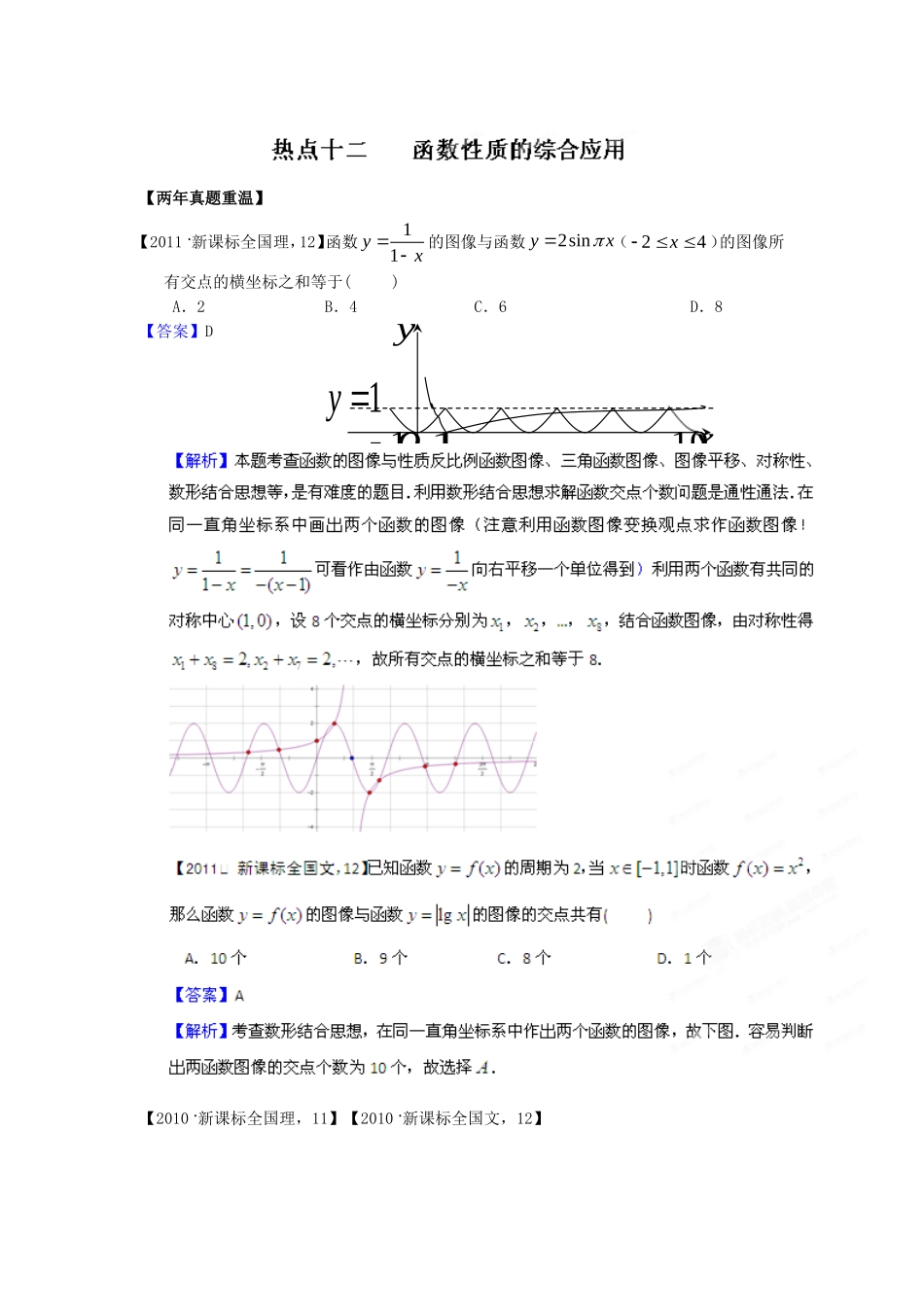
11xyo1y10【两年真题重温】【2011新课标全国理，12】函数11yx的图像与函数2sinyx（24x）的图像所有交点的横坐标之和等于()A．2B．4C．6D．8【答案】D【2010新课标全国理，11】【2010新课标全国文，12】已知函数|lg|,010,()16,10.2xxfxxx若,,abc互不相等，且()()(),fafbfc则abc的取值范围是(A)(1,10)(B)(5,6)(C)(10,12)(D)(20,24)【答案】C【解析】命题意图：本题主要考查分段函数、对数的运算性质以及利用数形结合解决问题的能力.作出函数()fx的图象如右图，不妨设abc，则1lglg10(0,1)2abc则(10,12)abcc.应选C.【命题意图猜想】【最新考纲解读】1．函数与方程①结合二次函数的图象，判断一元二次方程根的存在性及根的个数，从而了解函数的零点与方程根的联系．O120xy②根据具体函数的图象，能够借助计算器用二分法求相应方程的近似解，了解这种方法是求方程近似解的常用方法．2．函数模型及其应用①利用计算工具，比较指数函数、对数函数以及幂函数增长差异；结合实例体会直线上升、指数爆炸、对数增长等不同函数类型增长的含义．②收集一些社会生活中普遍使用的函数模型(指数函数、对数函数、幂函数、分段函数等)的实例，了解函数模型的广泛应用．③若()fx为偶函数，则()()(||)fxfxfx.④若奇函数()fx定义域中含有0，则必有(0)0f.2.函数的单调性1.函数单调性的定义：（1）如果函数xf对区间D内的任意21,xx，当21xx时都有21xfxf，则xf在D内是增函数；当21xx时都有21xfxf，则xf在D内是减函数.（2）设函数()yfx在某区间D内可导，若0fx，则()yfx在D内是增函数；若0fx，则()yfx在D内是减函数.2.单调性的定义（1）的等价形式：设baxx,,21，那么xfxxxfxf02121在,ab上是增函数；xfxxxfxf02121在,ab上是减函数；3.证明或判断函数单调性的方法：(1)定义法：设元作差变形判断符号给出结论.其关键是作差变形，为了便于判断差的符号，通常将差变成因式连乘积、平方和等形式，再结合变量的范围，假设的两个变量的大小关系及不等式的性质作出判断；①满足条件fxafbx的函数的图象关于直线2abx对称.②点(,)xy关于y轴的对称点为(,)xy；函数xfy关于y轴的对称曲线方程为xfy；(由分母为零确定)和直线ayc(由分子、分母中x的系数确定)，对称中心是点(,)dacc；⑧|()|fx的图象先保留()fx原来在x轴上方的图象，作出x轴下方的图象关于x轴的对称图形，然后擦去x轴下方的图象得到；(||)fx的图象先保留()fx在y轴右方的图象，擦去y轴左方的图象，然后作出y轴右方的图象关于y轴的对称图形得到.5.常见的图象变换特殊函数图象:(1)函数(0,)axbcxdycadbc:可由反比例函数(0)kykx图象平移、伸缩得到.图1示例.（3）函数F(x)＝f(x)－g(x)的零点就是方程f(x)＝g(x)的实数根，也就是函数y＝f(x)的图象与函数y＝g(x)的图象交点的横坐标．一般地，对于不能使用公式求根的方程f(x)＝0，我们可以将它与函数y＝f(x)联系起来，利用函数的图象、性质来求解．【方法技巧提炼】1.研究函数的性质要特别注意定义域优先原则.2.函数的单调性（1）定义法和导数法的选择.例2．已知函数f（x）＝xaxx22，),1[x．当a＝21时，求函数f（x）的最小值.【答案】10【解析】由(2)(2)fxfx，可知函数关于2x对称，同理由(7)(7)fxfx得到另外一条对称轴7x，由结论①可知2(72)10T.【点评】此例利用函数的对称轴的相关结论，得到函数的周期，体现了利用结论解题的重要性.(3)若已知类似函数周期定义式的恒等式，如何确定函数的周期？由周期函数的定义，采用迭代法可得结论：①函数()fx满足faxfx，则()fx是周期为2a的函数；②若1()(0)()fxaafx恒成立，则2Ta；③若fxafxa，则2Ta；④1()()1()fxfxafx，则4Ta.5.如何转换含有绝对值的函数【点评】此题通过去掉绝对值得到分段函数，利用图象进行判断.分类的标...