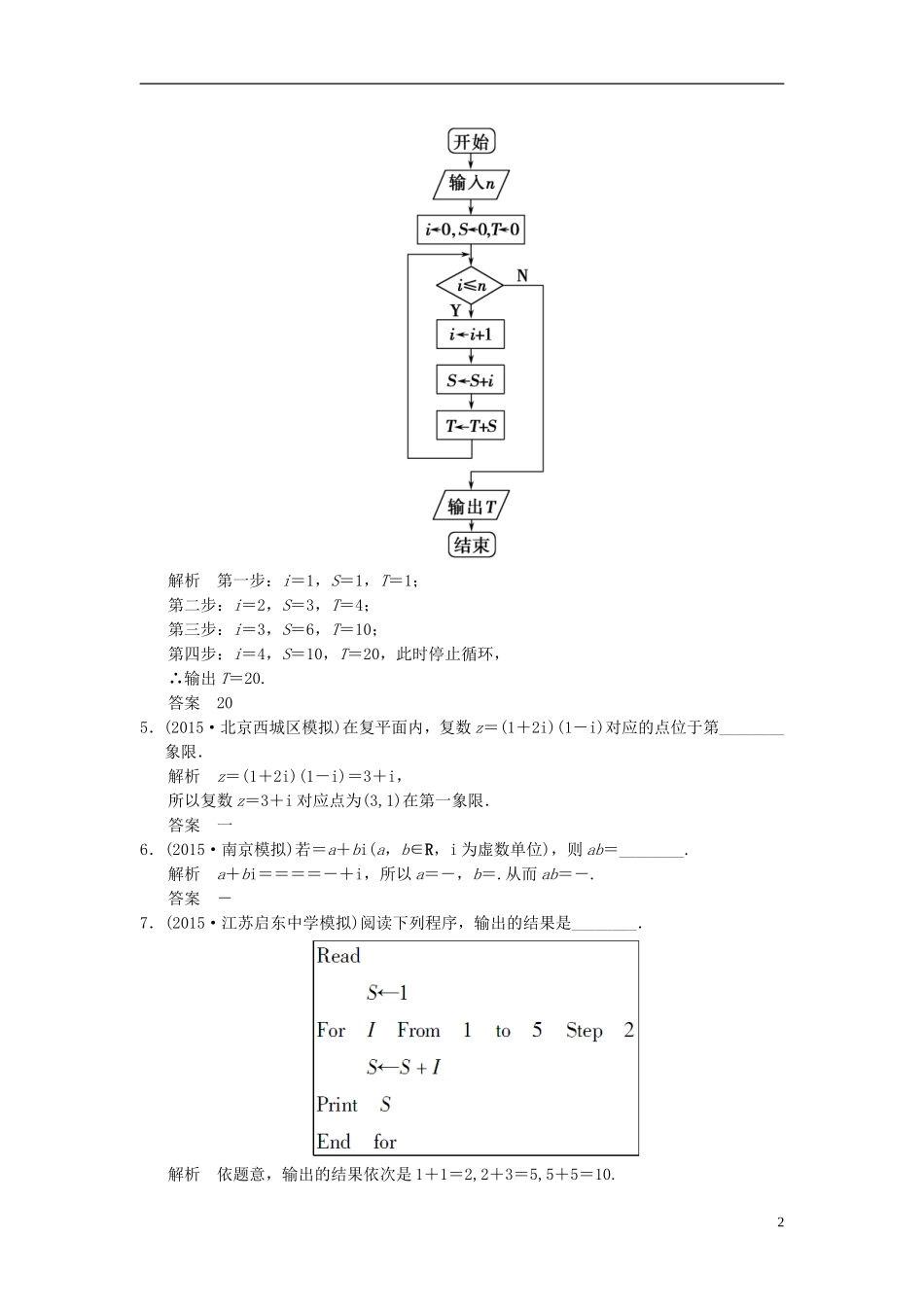
阶段回扣练13推理与证明、算法初步、复数B卷(建议用时:35分钟)1.(2014·苏州调研)设复数z满足zi=1+2i(i为虚数单位),则z的模为________.解析由|zi|=|1+2i|,得|z|==.答案2.(2014·北京卷)在(x+i)i=-1+2i(x∈R),则x=________.解析因为x+i==2+i,所以x=2.答案23.(2015·南京、盐城模拟)执行如图所示的流程图,则输出的k的值为________.解析逐次写出运行结果.该流程图运行4次,各次S的取值分别是1,2,6,15,所以输出的k=4.答案44.(2014·辽宁卷)执行如图所示的流程图,若输入n=3,则输出T=________.1解析第一步:i=1,S=1,T=1;第二步:i=2,S=3,T=4;第三步:i=3,S=6,T=10;第四步:i=4,S=10,T=20,此时停止循环,∴输出T=20.答案205.(2015·北京西城区模拟)在复平面内,复数z=(1+2i)(1-i)对应的点位于第________象限.解析z=(1+2i)(1-i)=3+i,所以复数z=3+i对应点为(3,1)在第一象限.答案一6.(2015·南京模拟)若=a+bi(a,b∈R,i为虚数单位),则ab=________.解析a+bi====-+i,所以a=-,b=.从而ab=-.答案-7.(2015·江苏启东中学模拟)阅读下列程序,输出的结果是________.解析依题意,输出的结果依次是1+1=2,2+3=5,5+5=10.2答案108.如图是一个算法的流程图,则输出S的值是________.解析执行过程如下表:S11+21=33+22=77+23=1515+24=3131+25=63n123451+2+22+…+24=31<33,输出S=1+2+22+…+25=63.答案639.已知数列{an}的各项分别为,,,,,,,,,,…,依它的前10项的规律,则a99+a100的值为________.解析通过将数列的前10项分组得到第一组有一个数:,分子、分母之和为2;第二组有两个数:,,分子、分母之和为3;第三组有三个数:,,,分子、分母之和为4;第四组有四个数,依次类推,a99,a100分别是第十四组的第8个数和第9个数,分子、分母之和为15,所以a99=,a100=.故a99+a100=.答案10.(2014·四川卷改编)执行如图的流程图,如果输入的x,y∈R,那么输出的S的最大值为________.解析本流程图的功能是当x,y满足约束条件时,求目标函数S=2x+y的最大值,如图所示,目标函数在点(1,0)处取得最大值2.答案2311.(2014·镇江调研)圆x2+y2=r2在点(x0,y0)处的切线方程为x0x+y0y=r2,类似地,可以求得椭圆+=1在(2,1)处的切线方程为________.解析由类比结构可知,相应的切线方程为:+=1,代入点坐标,所求切线方程为:+=1.答案+=112.(2015·苏州检测)对于不等式n2+n≤(n+1)2(n∈N*),某学生的证明过程如下:(1)当n=1时,12+1≤1+1,不等式成立.(2)假设n=k(k∈N*)时,不等式成立,即k2+k≤(k+1)2,则n=k+1时,(k+1)2+(k+1)=k2+3k+2<(k2+3k+2)+(k+2)=(k+2)2=[(k+1)+1]2,∴当n=k+1时,不等式也成立.对于上述证法,下列说法正确的序号是________.①过程全都正确;②n=1验证不正确;③归纳假设不正确;④从n=k到n=k+1的推理不正确.解析n=1的验证及归纳假设都正确,但从n=k到n=k+1的推理中没有使用归纳假设,而是通过不等式的放缩法直接证明,不符合数学归纳法的证题要求.答案④13.(2015·泰州检测)已知在等差数列{an}中,若m+2n+p=s+2t+r,m,n,p,s,t,r∈N*,则am+2an+ap=as+2at+ar,仿此类比,可得到等比数列{bn}中的一个正确命题:若m+2n+p=s+2t+r,m,n,p,s,t,r∈N*,则________.解析将等差数列项的和类比到等比数列项的积,得等比数列中的恒等式为bm(bn)2bp=bs(bt)2br.答案bm(bn)2bp=bs(bt)2br14.(2015·苏州模拟)观察:1-=1-+-=+1-+-+-=++……根据以上事实,由归纳推理可得,当n∈N*时,1-+-+…+-=(________)+…+.解析等式的左边“1-+-+…+-”中共有2014n项,其中间两项分别为和,由归纳推理可知,1-+-+…+-=++…+.答案4