椭圆双曲线复习VIP免费

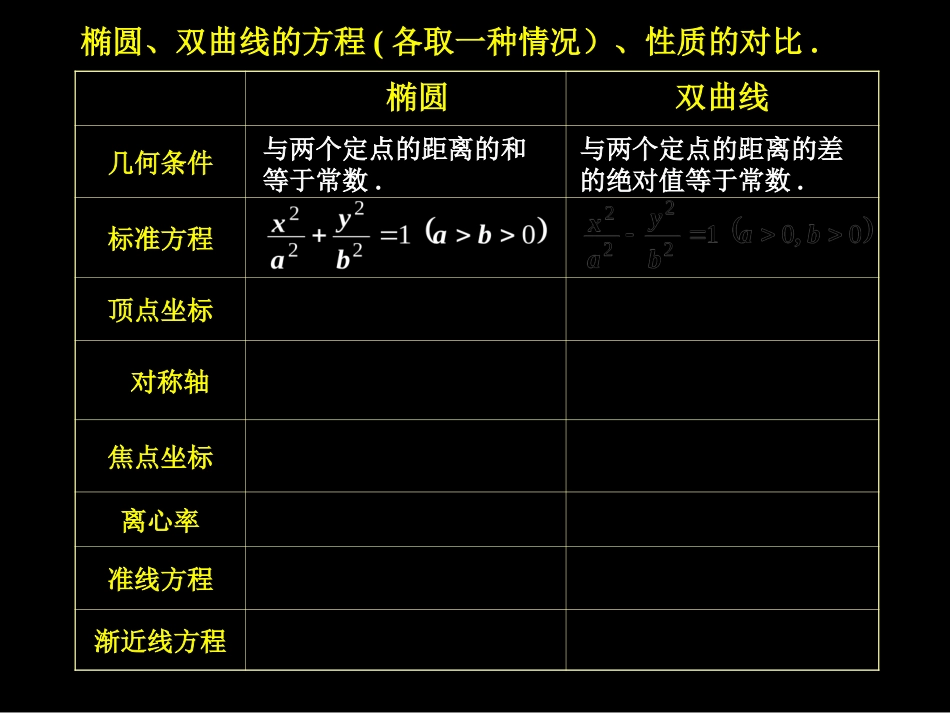
.F2F1yox.xF1F20y..椭圆、双曲线的方程(各取一种情况）、性质的对比.椭圆双曲线几何条件标准方程顶点坐标对称轴焦点坐标离心率准线方程渐近线方程与两个定点的距离的和等于常数.与两个定点的距离的差的绝对值等于常数.ba,,,000,abyax22短轴长轴，长轴长轴，byax22虚轴长轴，实轴长轴，220bacc,,220bacc,,10e1ecax2cax2xaby焦点访谈找出下列椭圆或双曲线的焦点坐标.0225259122yx192522yx准方程分析：将原方程变为标,,92522ba16222bac即.0404，，，焦点坐标为03694222yx材料一：焦点位置19422xy准方程分析：将原方程变为标,,9422ba13222bac即.130130，，，焦点坐标为11222mymx已知方程⑴表示焦点在x轴上的双曲线，求m的范围.分析：,0102mm.轴上时双曲线焦点在xm1⑵表示焦点在x轴上的椭圆，求m的范围.分析：,120102mmmm.轴上时椭圆焦点在xm123判断焦点位置.,的系数化为标准方程，观察22yx共同点：差异：椭圆看大小，双曲线看符号.探索：.,点三角形为此椭圆或双曲线的焦，则称长轴或实轴端点除外双曲线上一点是椭圆或焦点，为椭圆或双曲线的两个设2121FPFPFF焦点三角形.,点三角形为此椭圆或双曲线的焦，则称长轴或实轴端点除外双曲线上一点是椭圆或焦点，为椭圆或双曲线的两个设2121FPFPFF焦点三角形.____212122214812449PFFPFPFPyxFF，则椭圆上且满足在的两个焦点，是椭圆，已知材料二：xF1F20y..P..____21212221601169PFPFPFFPyxFF，则双曲线上且满足在的两个焦点，是双曲线，已知类比：6490y..F2F1oxP.，，设长轴端点除外是椭圆上一点焦点，的两个是椭圆，已知2122222101PFFPbabyaxFF)(探索：类比：,)(,实轴端点除外是双曲线上一点的两个焦点，是双曲线，已知PbabyaxFF001222221cos122bcos122b共同点：.中利用余弦定理求解都是在21FPF差异：；椭圆aPFPF221.aPFPF221双曲线.____________21PFPF则._________2121PFPFPFF，则设xF1F20y..P.焦点弦材料三：.的长两点，求弦、交椭圆于的右焦点，过椭圆的直线已知斜率为ABBAyxl12122分析：.,,,2211yxByxABA坐标分别为、设，方程为，，右焦点101xylF，由22122yxxy.0432xx得.,0342121xxxx2121xxkAB21221241xxxxk324xyF0..AB思考：以线段AB为直径的圆，与椭圆相应准线是何位置关系？.P相离.Fyox.AB.P以过椭圆的焦点的弦为直径的圆，和该焦点相应准线是何位置关系？类比：以过双曲线的焦点的弦为直径的圆，和该焦点相应准线是何位置关系？探索：相交P.AB.xF0y.mnd共同点：利用第二定义解题.差异：.,110ee双曲线椭圆相离三、小结提高焦点位置访谈核心知识方法思想••焦点弦焦点焦点三角形椭圆、双曲线的方程、性质四、作业1、课本复习参考题八的8、9、10.2、试给出访谈二中，与焦点三角形有关问题的一个探索.探索：以过椭圆的焦点的弦为直径的圆，和该焦点相应准线是何位置关系？以过双曲线的焦点的弦为直径的圆，和该焦点相应准线是何位置关系？类比：22120121211006460yxFFPFPFFPF.已知，是椭圆的两个焦点，是椭圆上任一点，且，求的面积分析：由探索1可知cos12221bPFPF601642cos325621212121PFFPFPFSPFFsin233256216433.2212121916643yxFFPPFPF已知，是双曲线的两个焦点，是双曲线上任意一点，若，则3316探索2：类比：.______21FPFS则