二次函数讲义-有例题讲解和作业VIP免费

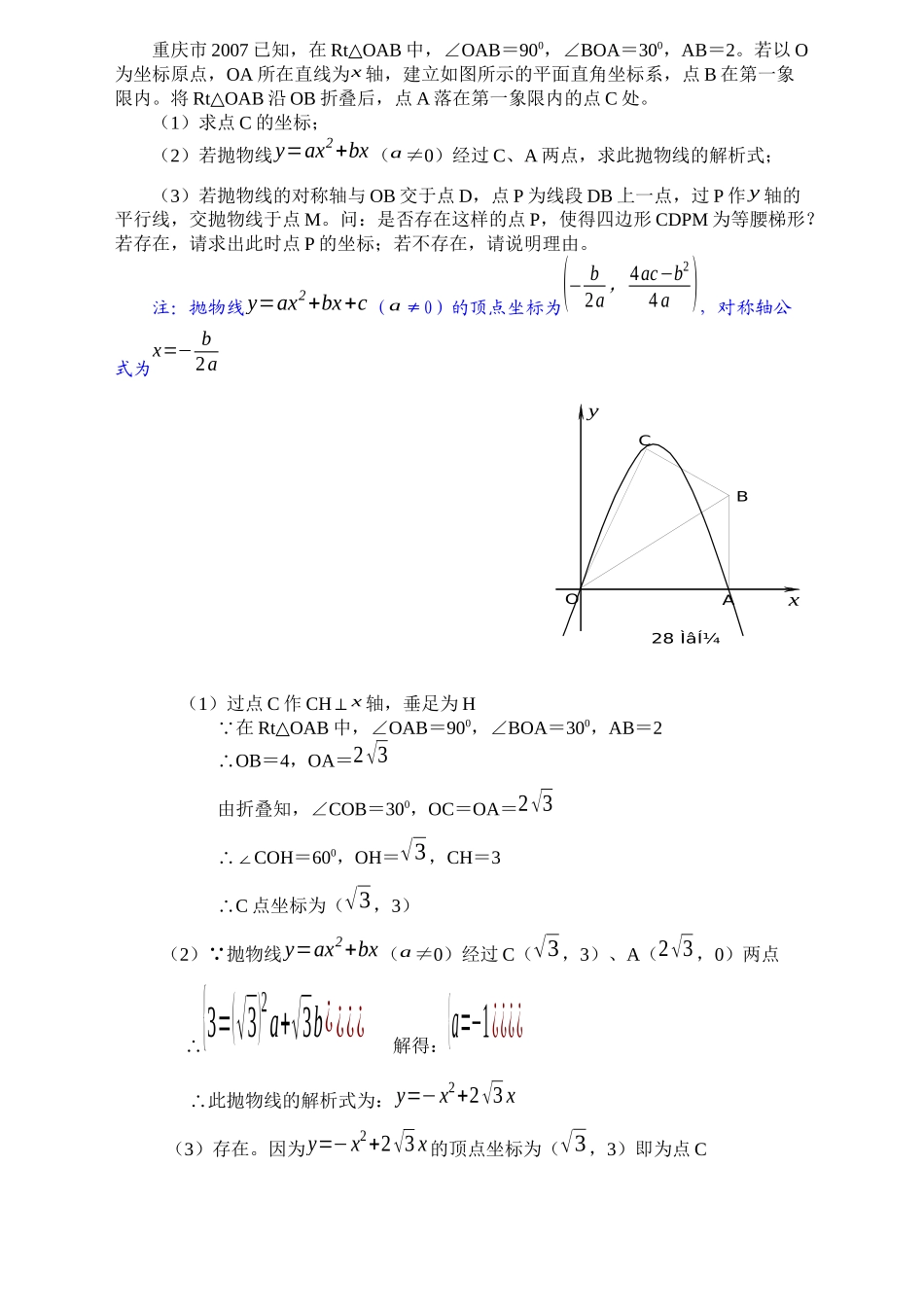
一、二次函数的概念1、定义：一般地，如果y=ax2+bx+c(a,b,c是常数，a≠0)，那么y叫做x的二次函数.2、注意点：（1）二次函数是关于自变量x的二次式，二次项系数a必须为非零实数，即a≠0，而b、c为任意实数。（2）当b=c=0时，二次函数y=ax2是最简单的二次函数。（3）二次函数y=ax2+bx+c(a,b,c是常数，a≠0)自变量的取值为全体实数（ax2+bx+c为整式）3、三种函数解析式：（1）一般式：y=ax2+bx+c（a≠0），对称轴：直线x=−b2a顶点坐标：(−b2a，4ac−b24a)（2）顶点式：y=a(x−h)2+k（a≠0），对称轴：直线x=h顶点坐标为（h,k）（3）交点式：y=a（x-x1）（x-x2）（a≠0）,对称轴:直线x=x1+x22(其中x1、x2是二次函数与x轴的两个交点的横坐标).二、二次函数的图象1、二次函数y=ax2+bx+c的图像是对称轴平行于（包括重合）y轴的抛物线.2、二次函数由特殊到一般，可分为以下几种形式：①y=ax2；②y=ax2+k；③y=a(x−h)2；④y=a(x−h)2+k；⑤y=ax2+bx+c.注：二次函数的图象可以通过抛物线的平移得到3、二次函数y=ax2+bx+c的图像的画法因为二次函数的图像是抛物线，是轴对称图形，所以作图时常用简化的描点法和五点法，其步骤是：(1)先找出顶点坐标，画出对称轴；(2)找出抛物线上关于对称轴的四个点(如与坐标轴的交点等)；(3)把上述五个点按从左到右的顺序用平滑曲线连结起来.三、二次函数的性质函数解析式开口方向对称轴顶点坐标y=ax2当a>0时开口向上当a<0时开口向下x=0（y轴）（0,0）y=ax2+kx=0（y轴）(0,k)y=a(x−h)2x=h(h,0)y=a(x−h)2+kx=h(h,k)y=ax2+bx+cx=−b2a(−b2a，4ac−b24a)注：常用性质：1、开口方向：当a>0时，函数开口方向向上；当a<0时，函数开口方向向下；2、增减性：当a>0时，在对称轴左侧，y随着x的增大而减少；在对称轴右侧，y随着x的增大而增大；当a<0时，在对称轴左侧，y随着x的增大而增大；在对称轴右侧，y随着x的增大而减少；3、最大或最小值：当a>0时，函数有最小值，并且当x=−b2a，y最小＝4ac−b24a当a<0时，函数有最大值，并且当x=−b2a，y最大＝4ac−b24a例题精讲1关于抛物线y=ax2+bx+c（a≠0），下面几点结论中，正确的有（）①当a0时，对称轴左边y随x的增大而减小，对称轴右边y随x的增大而增大，当a0时，情况相反.②抛物线的最高点或最低点都是指抛物线的顶点.③只要解析式的二次项系数的绝对值相同，两条抛物线的形状就相同.④一元二次方程ax2+bx+c=0（a≠0）的根，就是抛物线y=ax2+bx+c与x轴交点的横坐标.A.①②③④B.①②③C.①②D.①重庆市2007已知，在RtOAB△中，∠OAB＝900，∠BOA＝300，AB＝2。若以O为坐标原点，OA所在直线为x轴，建立如图所示的平面直角坐标系，点B在第一象限内。将RtOAB△沿OB折叠后，点A落在第一象限内的点C处。（1）求点C的坐标；（2）若抛物线y=ax2+bx（a≠0）经过C、A两点，求此抛物线的解析式；（3）若抛物线的对称轴与OB交于点D，点P为线段DB上一点，过P作y轴的平行线，交抛物线于点M。问：是否存在这样的点P，使得四边形CDPM为等腰梯形？若存在，请求出此时点P的坐标；若不存在，请说明理由。注：抛物线y=ax2+bx+c（a≠0）的顶点坐标为(−b2a，4ac−b24a)，对称轴公式为x=−b2ayxCBAO28Ìâͼ（1）过点C作CH⊥x轴，垂足为H 在RtOAB△中，∠OAB＝900，∠BOA＝300，AB＝2OB∴＝4，OA＝2√3由折叠知，∠COB＝300，OC＝OA＝2√3COH∴∠＝600，OH＝√3，CH＝3C∴点坐标为（√3，3）（2） 抛物线y=ax2+bx（a≠0）经过C（√3，3）、A（2√3，0）两点∴{3=(√3)2a+√3b¿¿¿¿解得：{a=−1¿¿¿¿∴此抛物线的解析式为：y=−x2+2√3x（3）存在。因为y=−x2+2√3x的顶点坐标为（√3，3）即为点CMP⊥x轴，设垂足为N，PN＝t，因为∠BOA＝300，所以ON＝√3tP∴（√3t，t）作PQCD⊥，垂足为Q，MECD⊥，垂足为E把x=√3⋅t代入y=−x2+2√3x得：y=−3t2+6tM∴（√3t，−3t2+6t），E（√3，−3t2+6t）同理：Q（√3，t），D（√3，1）要使四边形CDPM为等腰梯形，只需CE＝QD即3−(−3t2+6t)=t−1，解得：t1=43，t2=1（舍）P∴点坐标为（43√3，43）∴存在满足条件的点P，使得四边形CDPM为等腰梯形，此时P点的坐为（43√3，43）yxNHD...