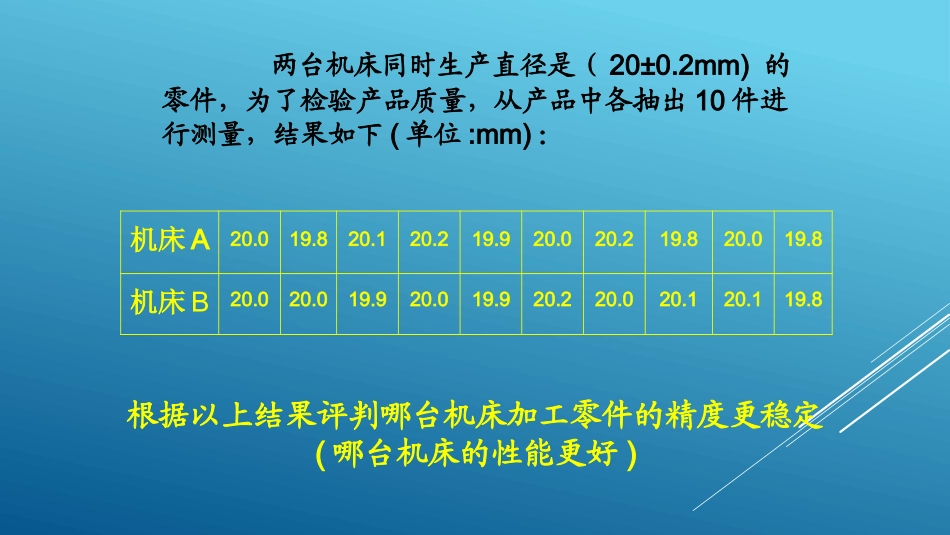
第一课时考察一组数据的集中趋势平均数众数中位数两台机床同时生产直径是(20±0.2mm)的零件,为了检验产品质量,从产品中各抽出10件进行测量,结果如下(单位:mm):机床A20.019.820.120.219.920.020.219.820.019.8机床B20.020.019.920.019.920.220.020.120.119.8根据以上结果评判哪台机床加工零件的精度更稳定(哪台机床的性能更好)机床A20.019.820.120.219.920.020.219.820.019.8机床B20.020.019.920.019.920.220.020.120.119.8它们的中位数也都是20.00mm还能不能对两台机床的性能进行比较呢?xA=20.0+(0-0.2+0.1+0.2-0.1+0+0.2-0.2+0-0.2)=20.0mmxB=20.0+(0+0-0.1+0-0.1+0.2+0+0.1+0.1-0.2)=20.0mm101101这时就需考察数据的离散程度了.机床A19.819.920.020.120.2012345678910数据序号产品直径机床A20.019.820.120.219.920.020.219.820.019.8机床B20.020.019.920.019.920.220.020.120.119.8机床B19.819.920.020.120.2012345678910数据序号产品直径通过上图,可看出两组数据相对于平均数的偏离情况,即反映机床B的数据离散程度较小,所以机床B比机床A加工零件的精确度要好.如何用数量来刻画一组数据的离散情况呢?方差的定义:设在一组数据x1,x2,…,xn中,各数据与它们的平均数x的差的平方分别是(x1-x)2,(x2-x)2,…,(xn-x)2,那么用它们的平均数来衡量这组数据的波动大小,并把它叫做这组数据的方差.方差的公式:s2=1nx1-x()2+x2-x()2+...+xn-x()2[](偏差平方的平均数.)计算两组数据的方差:)(026.0])208.19()208.19()2020[(10122222mmsA)(012.0])208.19()2020()2020[(10122222mmsB∵s2A>s2B∴甲机床生产的10个零件的直径比乙机床生产的10个零件的直径波动要大S2甲>S2乙波动大波动小较整齐不整齐1、样本7、8、8、6、6的方差是.X=7S2=[(7-7)2+(8-7)2+(8-7)2+(6-7)2+(6-7)2]5=0.82、为了考察甲、乙两种小麦的长势,分别从中抽出10株苗,测得苗高如下(单位:cm):甲:12131415101613111511乙:111617141319681016哪种小麦长得比较整齐?小结:1.方差:各数据与平均数的差的平方的平均数叫做这组数据的方差.2.方差的意义:用来衡量一批数据的离散程度(即这组数据偏离平均数的大小).即方差越大,说明数据的波动越大,越不稳定.计算一组数据的方差的一般步骤:1、利用平均数公式计算这组数据的平均数x2、利用方差公式计算这组数据的方差s2布置作业课堂作业:P132练习;家庭作业:(1)P137习题第10题;(2)预习下一节内容.