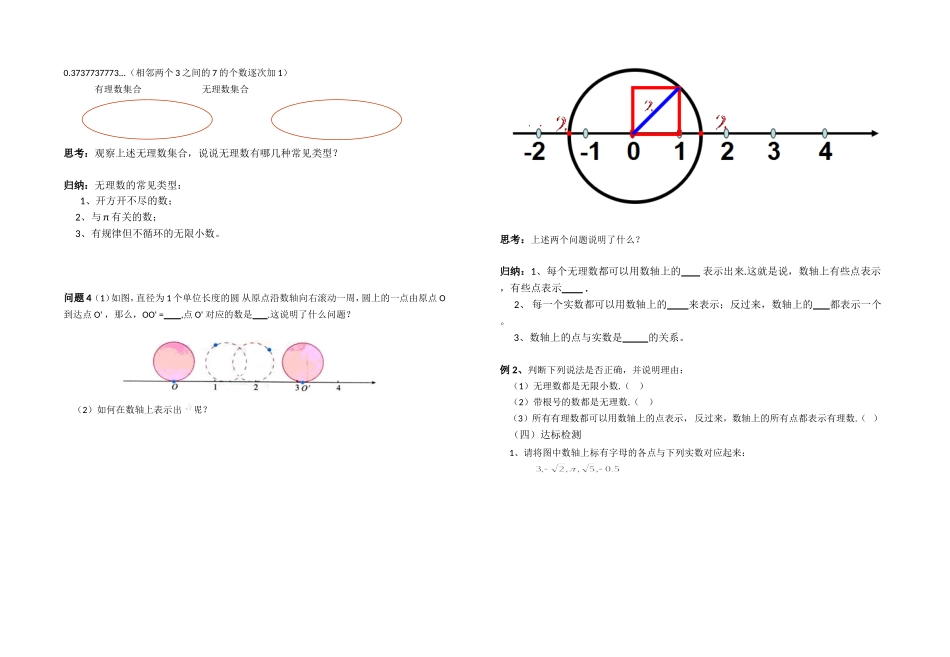
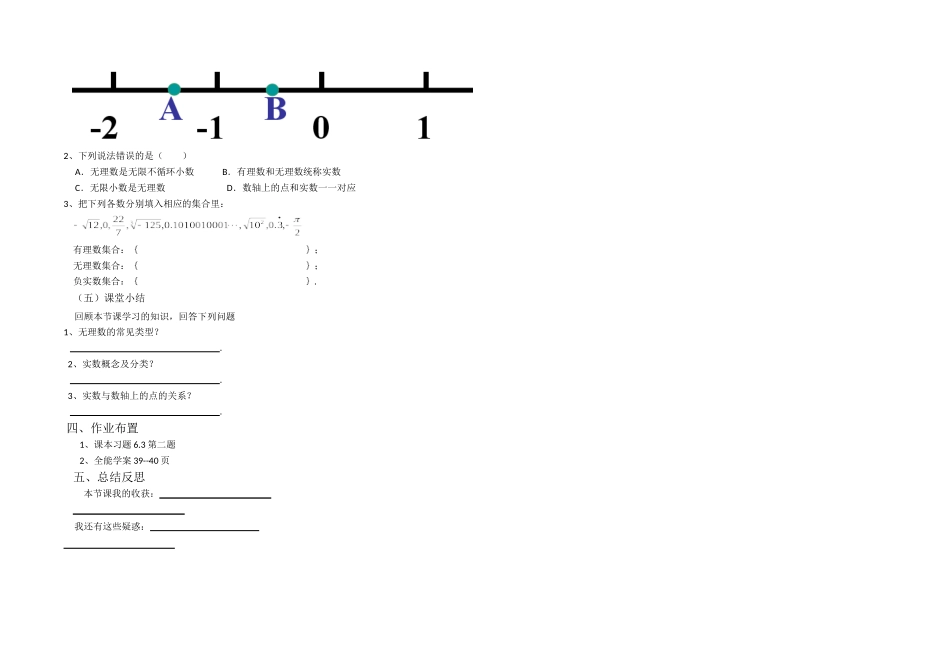
6.3实数(第1课时)一、教学目标1、了解无理数和实数的概念,掌握无理数的特征,并会进行分类;2、知道实数与数轴上的点具有一一对应关系,初步体会“数形结合”的数学思想。二、教学重难点1、重点:无理数和实数的概念,实数与数轴上点的对应关系;2、难点:无理数的特征以及对无理数的认识。三、教学过程(一)知识检测1、有理数的定义:和统称为有理数。2、有理数的分类:(1)按定义分类:(2)按大小分类:(二)情境导入问题1你能把下列分数写成小数形式吗?思考:3可以写成小数形式吗?归纳:任何一个有理数都可以写成有限小数或无线循环小数的形式;反过来,任何.或也都是有理数.(三)新知探究问题2你认为小数除了上述类型外,还会有什么类型的小数?这是我们以前学习的一些数,你知道它们是多少吗?这些数字有什么特征?思考:这里为什么用“≈”而不用“=”呢?不难发现,上面这些数都是小数。归纳:无理数------又叫无理数。实数------和统称为实数。问题3数字体系在慢慢扩大,引入实数这个概念后,你能给它进行分类吗?(1)按定义分类:(2)按大小分类:实数实数例1、把下列各数分别填在相应的集合中:,41,23,7,,25,2,320,5,83,94,00.3737737773...(相邻两个3之间的7的个数逐次加1)有理数集合无理数集合思考:观察上述无理数集合,说说无理数有哪几种常见类型?归纳:无理数的常见类型:1、开方开不尽的数;2、与π有关的数;3、有规律但不循环的无限小数。问题4(1)如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点O到达点O',那么,OO'=,点O'对应的数是.这说明了什么问题?(2)如何在数轴上表示出呢?思考:上述两个问题说明了什么?归纳:1、每个无理数都可以用数轴上的表示出来.这就是说,数轴上有些点表示,有些点表示.2、每一个实数都可以用数轴上的来表示;反过来,数轴上的都表示一个。3、数轴上的点与实数是的关系。例2、判断下列说法是否正确,并说明理由:(1)无理数都是无限小数.()(2)带根号的数都是无理数.()(3)所有有理数都可以用数轴上的点表示,反过来,数轴上的所有点都表示有理数.()(四)达标检测1、请将图中数轴上标有字母的各点与下列实数对应起来:2、下列说法错误的是()A.无理数是无限不循环小数B.有理数和无理数统称实数C.无限小数是无理数D.数轴上的点和实数一一对应3、把下列各数分别填入相应的集合里:有理数集合:{};无理数集合:{};负实数集合:{}.(五)课堂小结回顾本节课学习的知识,回答下列问题1、无理数的常见类型?.2、实数概念及分类?.3、实数与数轴上的点的关系?.四、作业布置1、课本习题6.3第二题2、全能学案39--40页五、总结反思本节课我的收获:我还有这些疑惑: