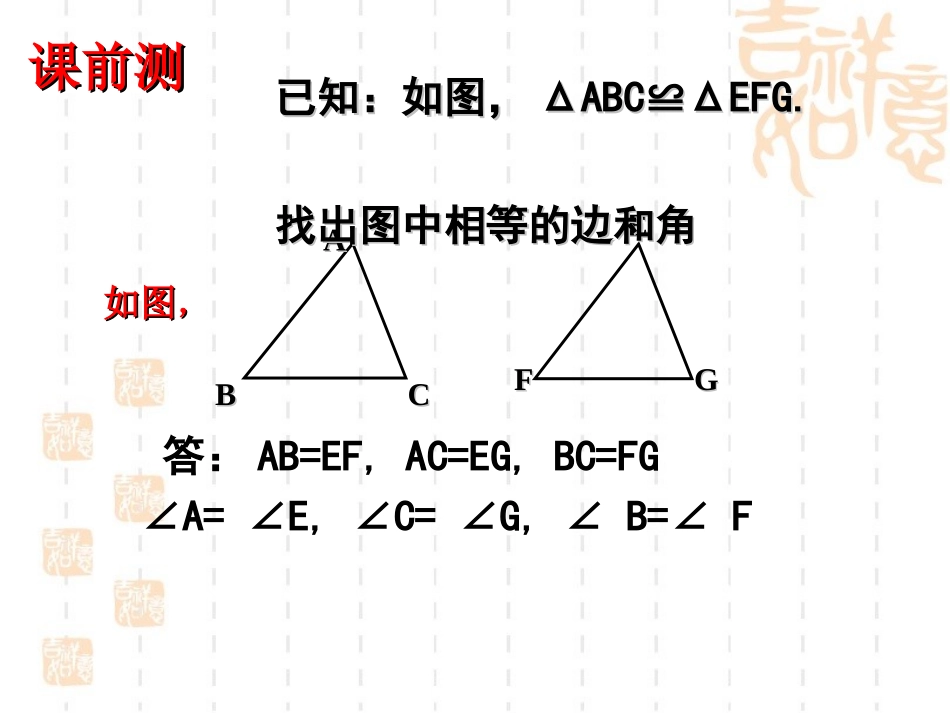
第四章三角形4.3.1探索三角形全等的条件如图如图,,AABBCCEEFFGG已知:如图,已知:如图,ΔΔABC≌ABC≌ΔΔEFG.EFG.找出图中相等的边和角找出图中相等的边和角答:AB=EF,AC=EG,BC=FG∠A=∠E,∠C=∠G,∠B=∠F课前测课前测我这里有一个三角形纸片,你能画一个三角形与它全等吗?如何画?需要几个与边或角的大小有关的条件?只知道一个条件行吗?两个条件呢?三个条件呢?让我们一起来探索三角形全等的条件想一想想一想•1、经历探索三角形全等条件的过程,体会分类思想•2、掌握三角形全等的“SSS”条件并会应用•3、掌握三角形的稳定性学习目标:学习目标:1.只给出一个条件(一条边或一个角)画三角形时,画出的三角形一定全等吗?(1)只给出一条边,如图3cm3cm3cm活动一活动一45◦45◦45◦1.只给出一个条件(一条边或一个角)画三角形时,画出的三角形一定全等吗?(2)只给出一条角,如图1)三角形的一个内角、一条边分别相等;2)三角形的两个内角分别相等;3)三角形的两条边分别相等.2.给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?•三角形的一个内角为30,一条边为3cm30◦3cm3cm3cm30◦30◦2.给出两个条件时,所画的三角形一定全等吗?30◦30◦50◦50◦2.给出两个条件时,所画的三角形一定全等吗?•如果三角形的两个内角分别是30,50时2.给出两个条件时,所画的三角形一定全等吗?如果三角形的两边分别为4cm,6cm时6cm6cm4cm4cm只给出一个条件或两个条件时,都不能保证所画出的三角形全等。3、若给出三个条件画三角形,你能说出有哪几种可能情况?1.都给角:给三个角2.都给边:给三条边3.既给角,又给边:(1)给一条边,两个角(2)给两条边,一个角(分类思想)已知一个三角形的三个内角分别为400,600,800,请画出这个三角形。结论:三个内角对应相等的两个三角形不一定全等.1.给出三个角040080060040060080已知三角形的三条边分别为4cm、5cm和7cm,请画出这个三角形。三边对应相等的两个三角形全等,简写为“边边边”或“SSS”7542.给出三条边三边对应相等的两个三角形全等,简写三边对应相等的两个三角形全等,简写为为““边边边边边边””或或““SSSSSS””。。用法:用法:AABBCCDDEEFF在△在△ABCABC和△和△DEFDEF中中 AB=DEAB=DEBC=EFBC=EFAC=DFAC=DF∴△∴△ABC≌△DEFABC≌△DEF((SSS)SSS)例1如图,当AB=CD,BC=DA时,图中的△ABC与△CDA是否全等?并说明理由。答:△ABC与△CDA是全等三角形。证明:在△ABC与△CDA中∴△ABC≌△CDA(SSS)DCBA AB=CDAD=CBAC=CA(已知)(已知)(公共边)例题精讲例题精讲答:能判定AB∥CD.如图,当AB=CD,BC=DA时,你能说明AB与CD、AD与BC的位置关系吗?为什么?DCBA1234变式训练变式训练∴∠3=∠4,∠1=∠2(全等三角形对应角相等)∴AB∥CD,AD∥BC(内错角相等,两直线平行)DCBA证明:在△ABC与△CDA中∴△ABC≌△CDA(SSS) AB=CDAD=CBAC=CA(已知)(已知)(公共边)1234变式训练变式训练1.两个锐角对应相等的两个直角三角形全等吗?为什么?答:不一定全等比如右边的两图,满足上述条件,但不全等练习练习2.已知:AC、BD相交于点O,且AB=DC,AC=DB,那么∠A=∠D吗?为什么?ODCBA答:我认为:∠A=∠D证明:在△ABC和△DCB中 )()()(公共边已知已知CBBCDBACDCAB∴△ABC≌△DCB(SSS)∴∠A=∠D(全等三角形的对应角相等)准备若干长度适中的小木条准备若干长度适中的小木条,,用其中用其中三根木条钉成一个三角形的框架,它的形三根木条钉成一个三角形的框架,它的形状和大小是固定的吗?如果用四根小木条状和大小是固定的吗?如果用四根小木条钉成的框架形状和大小固定吗?钉成的框架形状和大小固定吗?三角形的框架,它的大小和形状是固三角形的框架,它的大小和形状是固定不变的,三角形的这个性质叫做定不变的,三角形的这个性质叫做三角形的三角形的稳定性稳定性。。活动二活动二观察下图,这些图形的设计原理是什么?你还能举出一些其他的例子吗?只给出一个条件或两个条件时,都不能保证两个三角形全等。三个内角对应相等的两个三角形不一定全等。边边边公理:三边对应...