《全等三角形》VIP免费

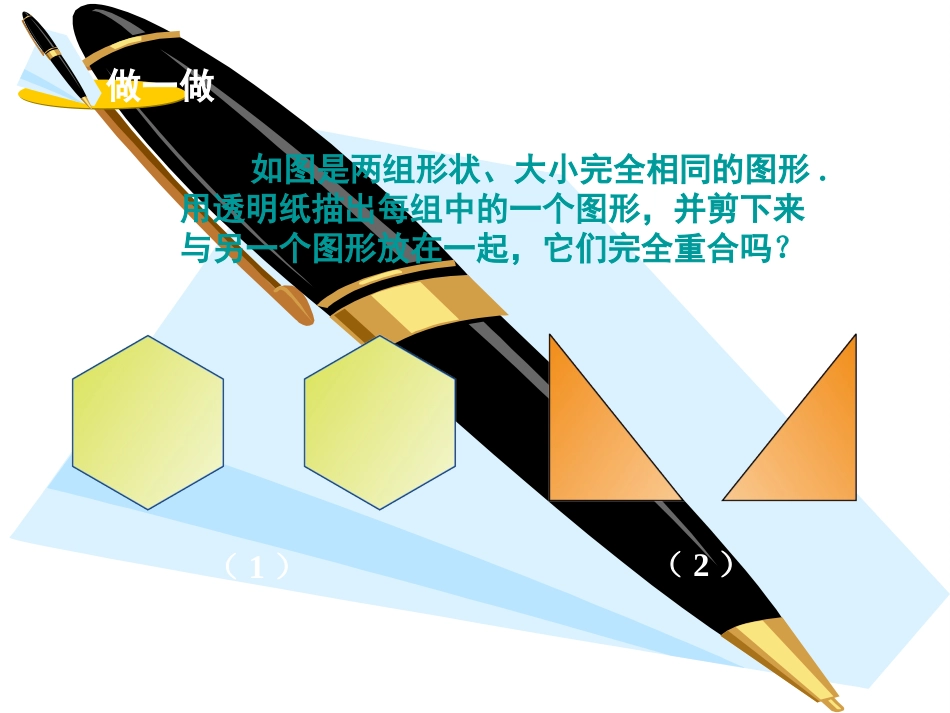
全等三角形全等三角形本课内容本节内容2.5如图是两组形状、大小完全相同的图形.用透明纸描出每组中的一个图形，并剪下来与另一个图形放在一起，它们完全重合吗？做一做（1）（2）（1）（2）我发现它们可以完全重合我发现它们可以完全重合结论我们把能够完全重合的两个图形叫作全等图形.我们把能够完全重合的两个图形叫作全等图形.动脑筋如图，△ABC分别通过平移、旋转、轴反射后得到△，问△ABC与△能完全重合吗？ABCABC根据平移、旋转和轴反射的性质，可知分别通过上述三个变换后得到的△与△ABC都可以完全重合，因此它们是全等图形.ABC结论能完全重合的两个三角形叫作全等三角形.能完全重合的两个三角形叫作全等三角形.全等三角形中，互相重合的顶点叫作对应顶点，互相重合的边叫作对应边，互相重合的角叫作对应角.A′B′C′ABCA(A′)B(B′)C(C′)例如，图（1）中的△ABC和△全等，ABC其中A与A′，B与B′，C与C′是对应顶点；记作：△ABC≌△.ABCAB与，BC与，CA与是对应边；ABBCCA∠A与∠A′，∠B与∠B′，∠C与∠C′是对应角.（1）小提示全等用符号“≌”表示，读作“全等于”.在表示两个三角形全等时，通常把表示对应顶点的字母写在对应位置上.结论全等三角形的对应边相等；全等三角形的对应边相等；全等三角形的对应角相等.全等三角形的对应角相等.我们知道，能够完全重合的两条线段是相等的，能够完全重合的两个角是相等的，由此得到：例如，A=AB=BC=C.,,AB=ABBC=BCCA=CA.,,举例例1如图，已知△ABC≌△DCB，AB=3，DB=4，∠A=60°.（1）写出△ABC和△DCB的对应边和对应角；（2）求AC，DC的长及∠D的度数.解（1）AB与DC，AC与DB，BC与CB是对应边；∠A与∠D，∠ABC与∠DCB，∠ACB与∠DBC是对应角.∴AC=DB=4，DC=AB=3.（2） AC与DB，AB与DC是全等三角形的对应边， ∠A与∠D是全等三角形的对应角，∴∠D=∠A=60°.练习如图，已知△ADF≌△CBE，AD=4，BE=3，AF=6，∠A=20°，∠B=120°.（1）找出它们的所有对应边和对应角；（2）求△ADF的周长及∠BEC的度数.解（1）AF与CE，AD与CB，DF与BE是对应边；∠A与∠C，∠AFD与∠CEB，∠D与∠B是对应角.（2）△ADF的周长是13，∠BEC=40°.两个三角形满足什么条件就能全等呢？下面我们就来探讨这个问题.每位同学在纸上的两个不同位置分别画一个三角形，它的一个角为50°，夹这个角的两边分别为2cm，2.5cm.将这两个三角形叠在一起，它们完全重合吗？由此你能得到什么结论？探究50°2cm2.5cm50°2cm2.5cm50°2cm2.5cm我发现它们完全重合，我猜测：有两边和它们的夹角分别相等的两个三角形全等.我发现它们完全重合，我猜测：有两边和它们的夹角分别相等的两个三角形全等.下面，我们从以下这几种情形来探讨这个猜测是否为真.设在△ABC和中，，ABC△ABC=ABCAB=ABBC=BC,.（1）△ABC和的位置关系如图.ABC△将△ABC作平移，使BC的像与重合，△ABC在平移下的像为.BCBCABC△由于平移不改变图形的形状和大小，因此△ABC≌△.ABC因为，ABC=ABC=ABCAB=AB=AB,所以线段A″B″与重合，AB因此点与点重合，AA那么与重合，ACACABC△ABC△所以与重合，因此，ABCABC△≌△从而ABCABC△≌△.（2）△ABC和的位置关系如图（顶点B与顶点重合）.ABC△因为，将△ABC作绕点B的旋转，旋转角等于，所以线段BC的像与线段重合.因为，所以(A)B(C)由于旋转不改变图形的形状和大小，又因为，BA=BA所以在上述旋转下，BA的像与重合，从而AC的像就与重合，于是△ABC的像就是因此△ABC≌△ABC.(A)B(C)（3）△ABC和的位置关系如图.△ABC根据情形（1），（2）的结论得将△ABC作平移，使顶点B的像和顶点重合，BBABCABC△≌△因此ABCABC.△≌△△ABC（4）△ABC和的位置关系如图.将△ABC作关于直线BC的轴反射，△ABC在轴反射下的像为△ABC.由于轴反射不改变图形的...