1.2极坐标系VIP免费

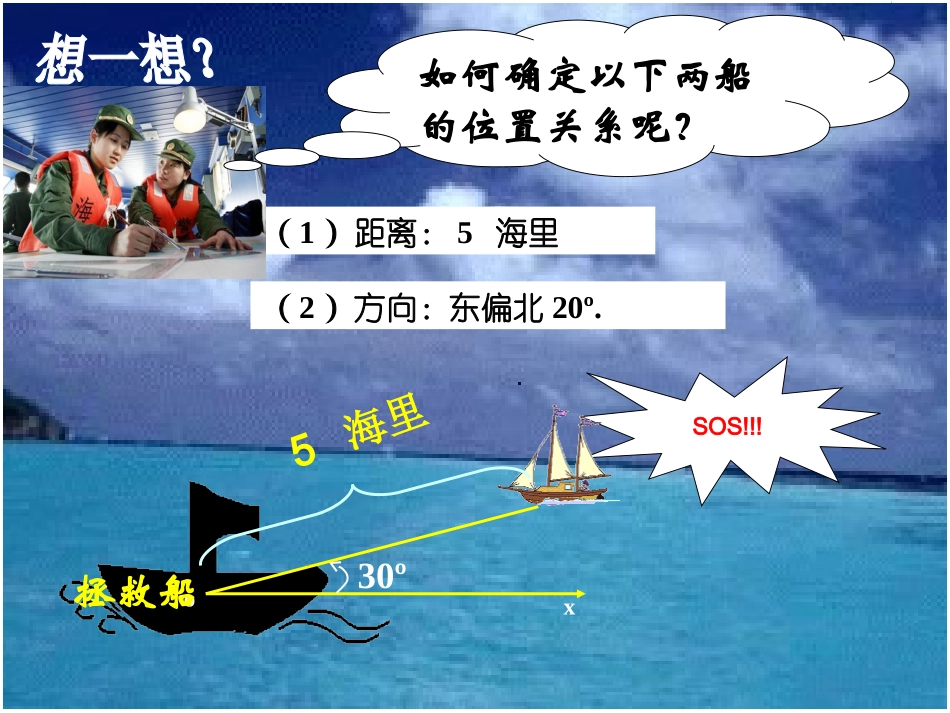
2025年1月12日极坐标系2.平面直角坐标系中的点P与坐标(a,b)是_____对应的.P(a,b).xyoab3.平面直角坐标系是最简单最常用的一种坐标系，但不是唯一的一种坐标系.有时用别的坐标系比较方便.我们先看下面的问题.还有什么坐标系呢？1.与角α终边相同的角：β=α+2kπ,kZ∈一一5海里（1）距离：5海里（2）方向：东偏北20º.ox拯救船30ºSOS!!!如何确定以下两船的位置关系呢？距离：4km方向：4xo以怀远路为X轴以丽子元北街为Y轴...请问：去育才中学怎么走？知识引入以丽子元北街为X轴以怀远路为Y轴...脑子进水了？从这向北2000米。请问：去育才中学怎么走？请分析上面这句话，他告诉了问路人什么？从这向北走2000米！出发点方向距离在生活中人们经常用方向和距离来表示一点的位置。这种用方向和距离表示平面上一点的位置的思想，就是极坐标的基本思想。在以上问题中，位置的确定是用什么方法确定的？距离与方向(1)在平面内取一个定点O，叫做极点；·o(2)引一条射线Ox，叫做极轴；x一、极坐标系的建立：(3)选定一个长度单位；(4)规定角度的正方向(通常取逆时针方向).θ这样建立的坐标系叫做极坐标系.二、极坐标系内一点的极坐标的规定XOM对于平面上任意一点M，用表示线段OM的长度，用表示从OX到OM的角度，叫做点M的极径，叫做点M的极角，有序数对（，）就叫做M的极坐标。特别强调：表示线段OM的长度，即点M到极点O的距离；表示从OX到OM的角度，即以OX（极轴）为始边，OM为终边的角。注意：极角一般是用弧度来表示题组一：说出下图中各点的极坐标ABCDEFGOX46535342(3,0)(6,2)(3,)245(5,)(3,)(4,)365(6,)3ABCDEFG题组二：在极坐标系里描出下列各点46535342ABCDEFGOX题组3.用点A,B,C,D,E分别表示教学楼,体育馆,图书馆,实验楼,办公楼的位置.建立适当的极坐标系,写出各点的极坐标.(O)xABCDE50m450600120m60m解:以点A为极点,AB所在的射线为极轴(单位长度为1m),建立极坐标系.则点A,B,C,D,E的极坐标分别为3(0,0),(60,0),(120,),(603,),(50,).324AB探究？①平面上一点的极坐标是否唯一？②若不唯一，那有多少种表示方法？③坐标不唯一是由谁引起的？④不同的极坐标是否可以写出统一表达式？极坐标系下的点与它的极坐标的对应情况特别规定：当M在极点时，它的极坐标=0，可以取任意值。在同一个极坐标系中，把下列的点表示出来1.(4,),(4,2),(4,4),(4,2)6666ABCD它们所表示的点有什么关系？你能体会极坐标与直角坐标系在刻画点的位置时的[思考]区别吗？三、点的极坐标的表达式的研究XOM如图：OM的长度为4，4请说出点M的极坐标的其他表达式。思：这些极坐标之间有何异同？思考：这些极角有何关系？这些极角的始边相同，终边也相同。也就是说它们是终边相同的角。本题点M的极坐标统一表达式：π42kπ+4，极径相同，不同的是极角四、极坐标系下点的极坐标OXPM探索点M（3，/4）的所有极坐标极径是正的时候：423k，探究①平面上一点的极坐标是否唯一？②若不唯一，那有多少种表示方法？③坐标不唯一是由谁引起的？④同一点不同的极坐标是否可以写出统一表达式？不唯一有无数种极角可以（ρ，2kπ+θ）OXPM(ρ,θ)…五、极坐标系下点与它的极坐标的对应情况[1]给定（,）,就可以在极坐标平面内确定唯一的一点M。[2]给定平面上一点M，但却有无数个极坐标与之对应。原因在于：极角有无数个。一般地,若(ρ,θ)是一点的极坐标,则(ρ,θ+2kπ)、都可以作为它的极坐标.如果限定ρ＞0,0≤θ＜2π或－π＜θ≤π,那么除极点外,平面内的点和极坐标就可以一一对应了.2.在极坐标系中,与(ρ,θ)关于极轴对称的点是()A.(ρ,θ)B.(ρ,－θ)C.(ρ,θ＋π)D.(ρ,π－θ)AB题组四1.在极坐标系中，与点(3,)重合的点是()6A.(3,)B.(3,－)C.(3,)D.(3,－)1366176653.边长为a的正六边形OABCDE在极坐标系中的位置如图所示，求这个正六边形各顶点的极坐标。ABCxEDOO(0,0)，C(2a,0)11π(3,),6Baπ(3,),6Da5π(,)3Aaπ(,)3Ea(1)(2)(3)(,)(0,ππ)AAAA点关于极轴对称的...