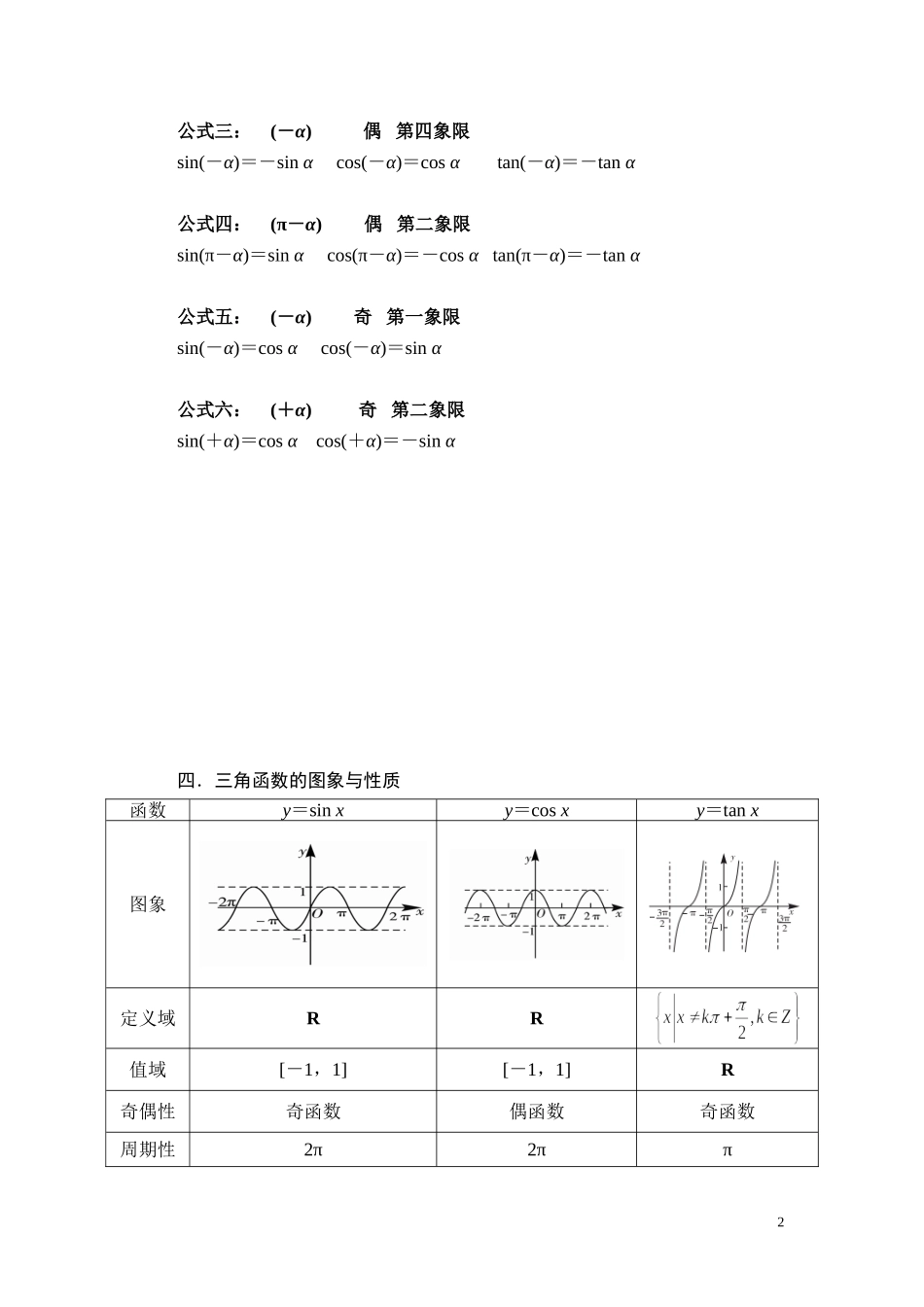
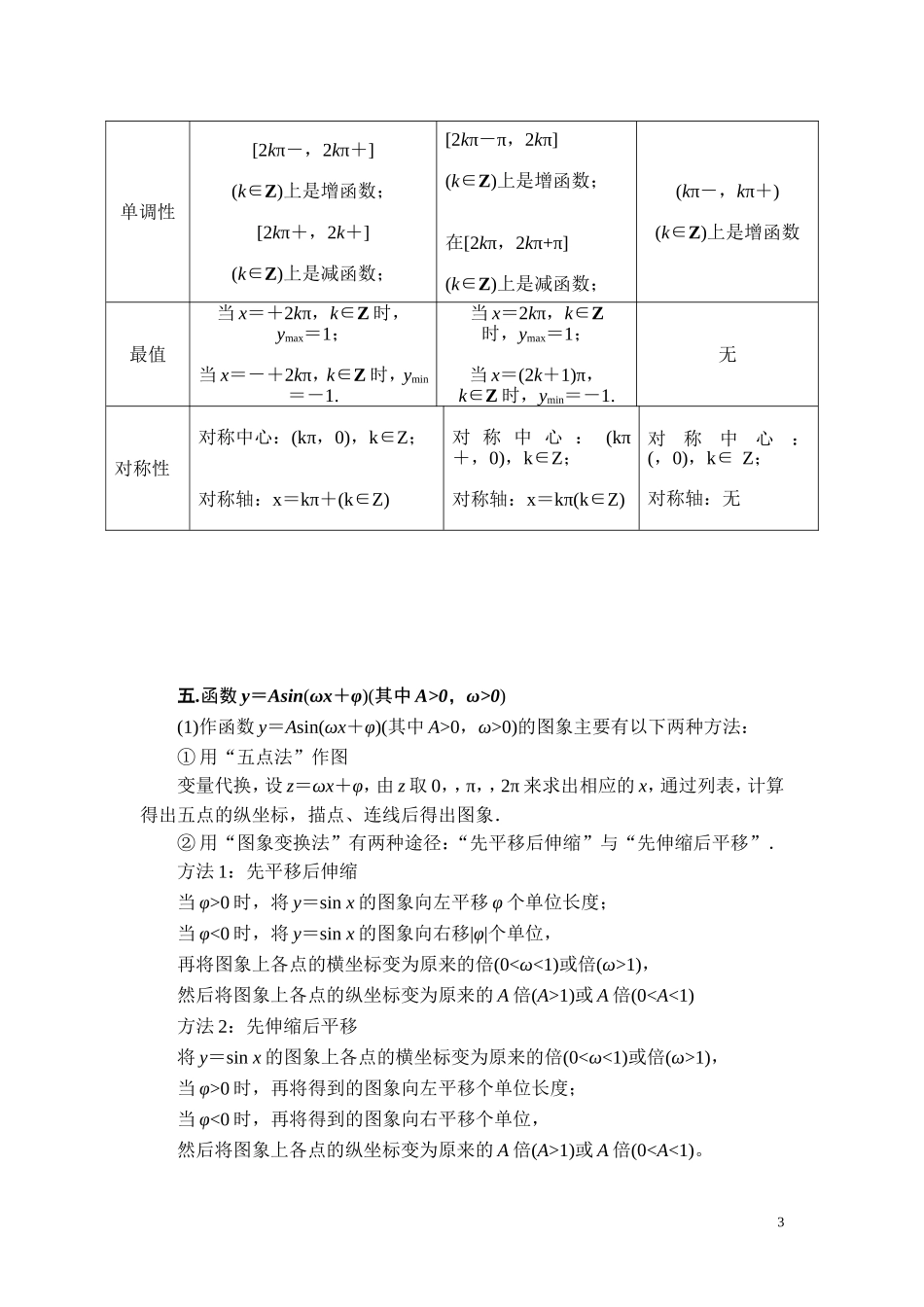
《三角》知识要点一.任意角和弧度制1,角可看成是平面内一射线绕端点从一个位置旋转到另一个位置所成图形.按旋转方向可分为正角、负角、零角;按终边落在平面直角坐标系中的位置,可分为象限角、轴线角.2,凡是与角α终边相同的角,都可以表示成α+k·360°(k∈Z)的形式.特例:终边在x轴上的角的集合为{α|α=k·180°,k∈Z};终边在y轴上的角的集合为{α|α=90°+k·180°,k∈Z};终边在坐标轴上的角的集合为{α|α=k·90°,k∈Z}.3,在弧度制下,其中α(0<α<2π)为弧所对圆心角的弧度数.扇形的弧长公式为l=α·R,扇形的面积公式为S=lR=αR2,二.任意角的三角函数1,设P(x,y)是角α的终边上任意一点(与原点不重合),记r=|OP|=,则sinα=,cosα=,tanα=(x≠0).2.特殊角三角函数值3.同角三角函数的基本关系(1)平方关系:sin2α+cos2α=1;(2)商数关系:=tanα.三.诱导公式法则:奇变偶不变;符号看象限。公式一:(α+2kπ)k∈Z偶第一象限sin(α+2kπ)=sinα,cos(α+2kπ)=cosα,tan(α+2kπ)=tanα,公式二:(π+α)偶第三象限sin(π+α)=sinαcos(π+α)=cosαtan(π+α)=tanα1公式三:(-α)偶第四象限sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanα公式四:(π-α)偶第二象限sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanα公式五:(-α)奇第一象限sin(-α)=cosαcos(-α)=sinα公式六:(+α)奇第二象限sin(+α)=cosαcos(+α)=-sinα四.三角函数的图象与性质函数y=sinxy=cosxy=tanx图象定义域RR值域[-1,1][-1,1]R奇偶性奇函数偶函数奇函数周期性2π2ππ2单调性[2kπ-,2kπ+](k∈Z)上是增函数;[2kπ+,2k+](k∈Z)上是减函数;[2kπ-π,2kπ](k∈Z)上是增函数;在[2kπ,2kπ+π](k∈Z)上是减函数;(kπ-,kπ+)(k∈Z)上是增函数最值当x=+2kπ,k∈Z时,ymax=1;当x=-+2kπ,k∈Z时,ymin=-1.当x=2kπ,k∈Z时,ymax=1;当x=(2k+1)π,k∈Z时,ymin=-1.无对称性对称中心:(kπ,0),k∈Z;对称轴:x=kπ+(k∈Z)对称中心:(kπ+,0),k∈Z;对称轴:x=kπ(k∈Z)对称中心:(,0),k∈Z;对称轴:无五.函数y=Asin(ωx+φ)(其中A>0,ω>0)(1)作函数y=Asin(ωx+φ)(其中A>0,ω>0)的图象主要有以下两种方法:①用“五点法”作图变量代换,设z=ωx+φ,由z取0,,π,,2π来求出相应的x,通过列表,计算得出五点的纵坐标,描点、连线后得出图象.②用“图象变换法”有两种途径:“先平移后伸缩”与“先伸缩后平移”.方法1:先平移后伸缩当φ>0时,将y=sinx的图象向左平移φ个单位长度;当φ<0时,将y=sinx的图象向右移|φ|个单位,再将图象上各点的横坐标变为原来的倍(0<ω<1)或倍(ω>1),然后将图象上各点的纵坐标变为原来的A倍(A>1)或A倍(0
1),当φ>0时,再将得到的图象向左平移个单位长度;当φ<0时,再将得到的图象向右平移个单位,然后将图象上各点的纵坐标变为原来的A倍(A>1)或A倍(00,ω>0,x∈[0,+∞))表示一个振动量时,A就表示这个振动量离开平衡位置的最大距离,通常把它叫做这个振动的振幅;往复振动一次所需要的时间T=,它叫做振动的周期;单位时间内往复振动的次数f==,它叫做振动的频率;ωx+φ叫做相位,φ叫做初相(即当x=0时的相位).《三角》知识要点一.任意角和弧度制1,角可看成是平面内一射线绕端点从一个位置旋转到另一个位置所成图形.按旋转方向可分为、、;按终边落在平面直角坐标系中的位置,可分为、.2,凡是与角α终边相同的角,都可以表示成的形式.特例:终边在x轴上的角的集合为;终边在y轴上的角的集合为;终边在坐标轴上的角的集合为.3,在弧度制下,其中α(0<α<2π)为弧所对圆心角的弧度数.扇形的弧长公式为l=,扇形的面积公式为S==,二.任意角的三角函数1,设P(x,y)是角α的终边上任意一点(与原点不重合),记r=|OP|=,则sinα=,cosα=,tanα=(x≠0).2...