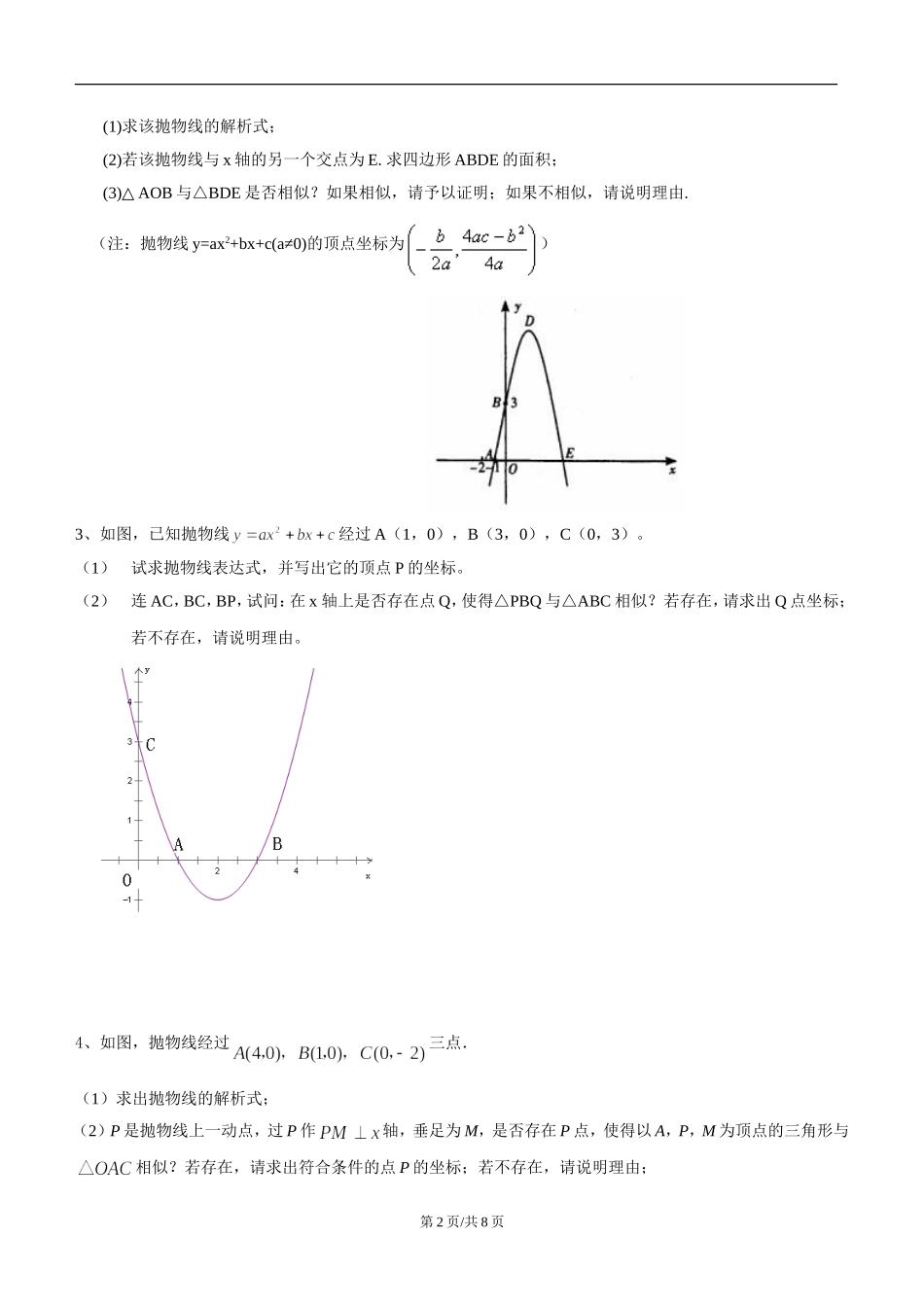
1、如图,已知抛物线的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.(1)试判断△AOC与△COB是否相似;(2)若点D是抛物线的顶点,DH垂直于x轴,垂足为H,试判断直角三角形DHA与直角三角形COB是否相似?说明理由.变式1:若点M在抛物线上且在x轴上方,过点M作MG垂直于x轴,垂足为点G,是否存在M,使得△AMG与△AOC相似.变式2:若点D是抛物线的顶点,点M在抛物线上且在x轴上方,过点M做x轴的垂线,垂足为点G,是否存在M,使得△AMG与△DCB相似.2、已知:如图,抛物线与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D.第1页/共8页(1)求该抛物线的解析式;(2)若该抛物线与x轴的另一个交点为E.求四边形ABDE的面积;(3)AOB△与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.(注:抛物线y=ax2+bx+c(a≠0)的顶点坐标为)3、如图,已知抛物线经过A(1,0),B(3,0),C(0,3)。(1)试求抛物线表达式,并写出它的顶点P的坐标。(2)连AC,BC,BP,试问:在x轴上是否存在点Q,使得△PBQ与△ABC相似?若存在,请求出Q点坐标;若不存在,请说明理由。4、如图,抛物线经过三点.(1)求出抛物线的解析式;(2)P是抛物线上一动点,过P作轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;第2页/共8页5、如图,在平面直角坐标系中,把抛物线向左平移1个单位,再向下平移4个单位,得到抛物线.所得抛物线与轴交于两点(点在点的左边),与轴交于点,顶点为.(1)写出的值;(2)判断的形状,并说明理由;(3)在线段上是否存在点,使∽?若存在,求出点的坐标;若不存在,说明理由.6、如图(1),直线y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.(1)求该抛物线的解析式;(2)在该抛物线的对称轴上是否存在点M,使以C、P、M为顶点的三角形为等腰三角形?若存在,请直接写出所有符合条件的点M的坐标;若不存在,请说明理由;(3)连结AC,在x轴上是否存在点Q,使以P、B、Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由;(4)当0<x<3时,在抛物线上求一点E,使△CBE的面积有最大值.第3页/共8页ADCBOxy(图(2)、图(3)供画图探究)7、如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.(1)当∠AOB=30°时,求弧AB的长度;(2)当DE=8时,求线段EF的长;(3)在点B运动过程中,是否存在以点E、C、F为顶点的三角形与△AOB相似,若存在,请求出此时点E的坐标;若不存在,请说明理由.第4页/共8页8、已知抛物线的顶点坐标为(4,-1),与y轴交于点C(0,3),O是原点.(1)求这条抛物线的解析式;(2)设此抛物线与轴的交点为A,B(A在B的左边),问在轴上是否存在点P,使以O,B,P为顶点的三角形与△AOC相似?若存在,请求出点P的坐标:若不存在,请说明理由.9、如图①,已知抛物线的顶点为A(2,1),且经过原点O,与x轴的另一交点为B.(1)求抛物线的解析式;(2)若点C在抛物线的对称轴上,点D在抛物线上,且以O、C、D、B四点为顶点的四边形为平行四边形,求D点的坐标;(3)连接OA、AB,如图②,在x轴下方的抛物线上是否存在点P,使得△OBP与△OAB相似?若存在,求出P点的坐标;若不存在,说明理由.第5页/共8页OBDECFxyAAABBOOxxyy图①图②10、如图,已知△ABC中,∠ACB=90°以AB所在直线为x轴,过c点的直线为y轴建立平面直角坐标系.此时,A点坐标为(-1,0),B点坐标为(4,0)(1)试求点C的坐标(2)若抛物线过△ABC的三个顶点,求抛物线的解析式.(3)点D(1,m)在抛物线上,过点A的直线y=-x-1交(2)中的抛物线于点E,那么在x轴上点B的左侧是否存在点P,使以P、B、D为顶点的三角形与△ABE相似?若存在,求出P点坐标;若不存在,说明理由.11、如图,四边形ABCD是平行四边形,AB=4,OB=2,抛物线过A、B、C三点,与x轴交于另一点D.一动点P...