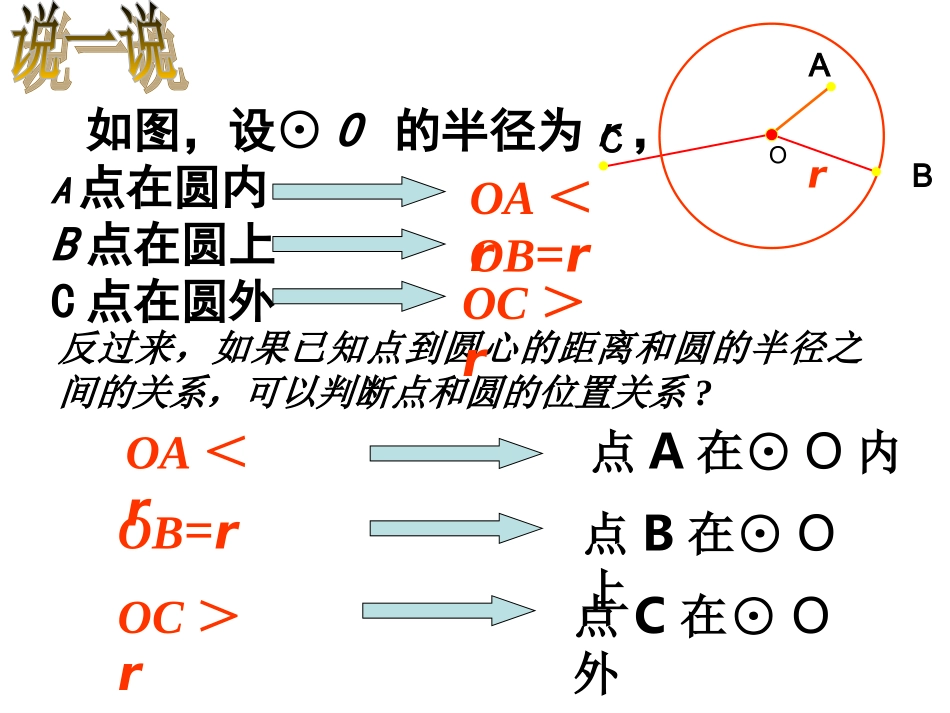
24.2.1点和圆的位置关系24.2.1点和圆的位置关系如图,设⊙O的半径为r,A点在圆内B点在圆上C点在圆外点A在⊙O内点B在⊙O上点C在⊙O外反过来,如果已知点到圆心的距离和圆的半径之间的关系,可以判断点和圆的位置关系?OA<rOB=rOC>rABCrOA<rOB=rOC>rO设⊙O的半径为r,点到圆心的距离为d。则点和圆的位置关系点在圆内dr﹤点在圆上点在圆外d=rd>r练习:已知圆的半径等于5厘米,若点到圆心的距离是:⑴8厘米⑵4厘米⑶5厘米。请你分别说出点与圆的位置关系。●●●●O符号读作“等价于”,它表示从符号的左端可以得到右端,从右端也可以得到左端.符号读作“等价于”,它表示从符号的左端可以得到右端,从右端也可以得到左端.圆外的点圆内的点圆上的点平面上的一个圆,把平面上的点分成三类:圆上的点,圆内的点和圆外的点。圆的内部可以看成是;圆的外部可以看成是。到圆心的距离大于半径的点的集合思考:平面上的一个圆把平面上的点分成哪几部分?到圆心的距离小于半径的点的集合问:⊙O的半径6cm,当OP=6时,点P在;当OP时点P在圆内;当OP时,点P不在圆外。圆上<6≤6A6O点A在点B在点C在 OA=8<10∴点A在圆内 OB=10=10∴点B在圆上 OC=12>10∴点C在圆外圆内圆上圆外1.O⊙的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:画出由所有到已知点O的距离大于或等于2CM并且小于或等于3CM的点组成的图形。OO问:如图已知矩形ABCD的边AB=3厘米,AD=4厘米ADCB(1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?(B在圆上,D在圆外,C在圆外)(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?(B在圆内,D在圆上,C在圆外)(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?(B在圆内,D在圆内,C在圆上)1.已知⊙O的面积为25π:(1)若PO=5.5,则点P在;(2)若PO=4,则点P在;(3)若PO=,则点P在圆上;(4)若点P不在圆外,则PO__________。随堂练习OO52.如图,⊿ABC中,∠C=90°,BC=3,AC=6,CD为中线,以C为圆心,以为半径作圆,则点A、B、D与圆C的关系如何?DCBA523随堂练习63已知菱形ABCD的对角线为AC和BD,E、F、G、H分别是AB、BC、CD、DA的中点,求证E、F、G、H四个点在同一个圆上。EFGHBACD思路:要证明几个点在同一圆上,就是证明这几个点到某一个定点的距离相等O问:在⊙O中,点M到⊙O的最小距离为3,最大距离是19,那么⊙O的半径为()ABOMBAOM11或8●A●A●B过一点可作几条直线?过两点可以作几条直线?过三点呢?过两点有且只有一条直线(直线公理)(“有且只有”就是“确定”的意思)经过一点可以作无数条直线;过三点1、若三点共线,则过这三点只能作一条直线.ABC2、若三点不共线,则过这三点不能作直线,但过任意其中两点一共可作三条直线.ABC直线公理:两点确定一条直线对于一个圆来说,过几个点能作一个圆,并且只能作一个圆?过一点能作几个圆?无数个A过A点的圆的圆心有何特点?平面上除A点外的任意一点经过一个已知点A能确定一个圆吗?A经过一个已知点能作无数个圆过两点能作几个圆?AB过A、B两点的圆的圆心有何特点?经过两点A,B的圆的圆心在线段AB的垂直平分线上.以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.●O●O经过两个已知点A、B能确定一个圆吗?AB经过两个已知点A、B能作无数个圆经过两个已知点A、B所作的圆的圆心在怎样的一条直线上?它们的圆心都在线段AB的中垂线上。ABC为什么过同一直线上的三点不能作圆呢?因为DE∥FG,所以没有交点,即没有过这三点的圆心DFEG1.当三点共线(不能作圆)参见课本P92反证法经过三个已知点A,B,C能确定一个圆吗?ABC1、连结AB,作线段AB的垂直平分线DE,ODEGF2、连结BC,作线段BC的垂直平分线FG,交DE于点O,3、以O为圆心,OB为半径作圆,作法:⊙O就是所求作的圆已知:不在同一直线上的三点A、B、C求作:⊙O,使它经过A、B、C2、当三点不共线请你证明你作的圆符合要求•证明: 点O在AB的垂直平分线上,•∴OA=OB.同理,OB=OC.∴OA=OB=OC.∴点A,B,C在以O为圆心,OA长为半径的圆上....