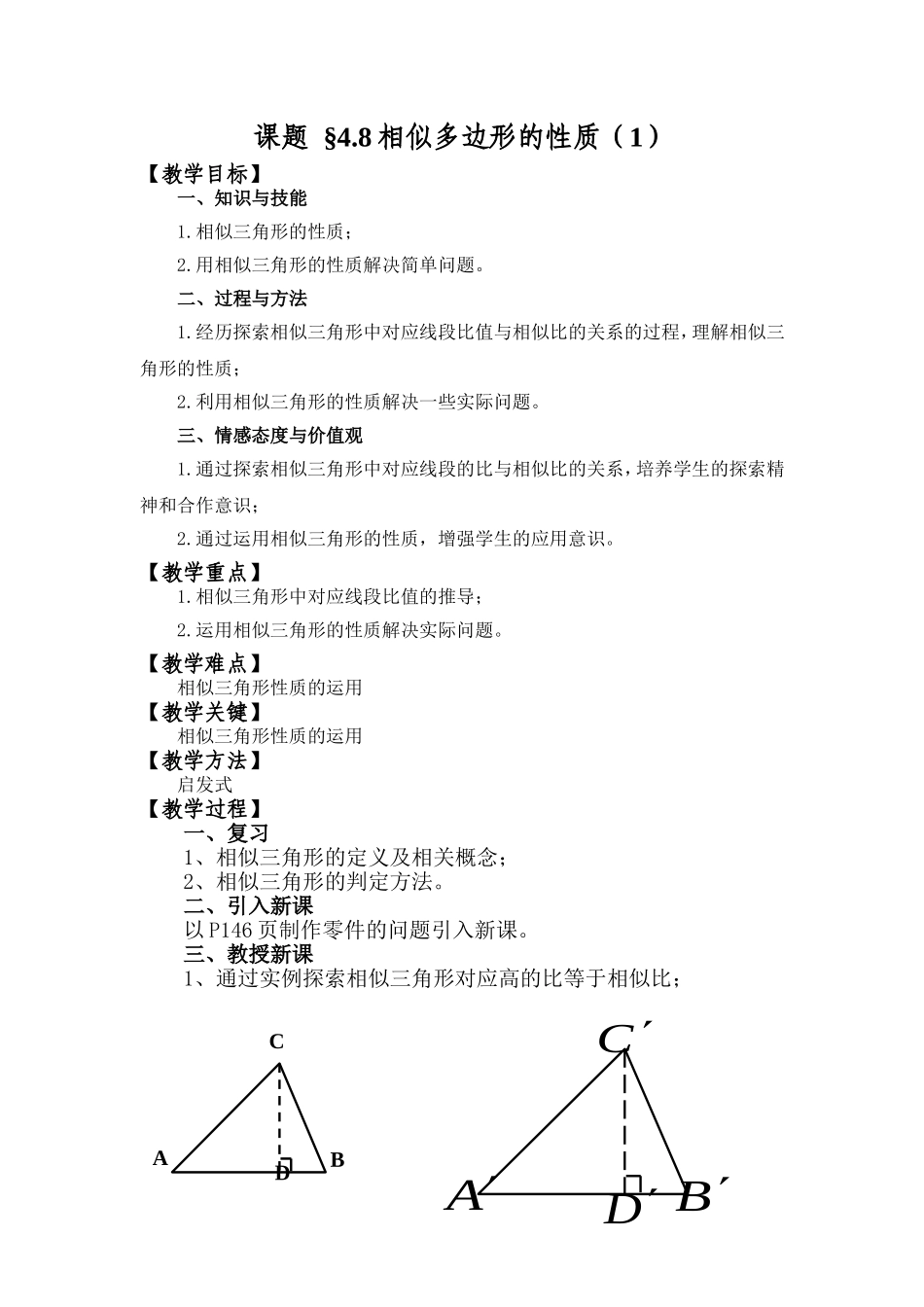
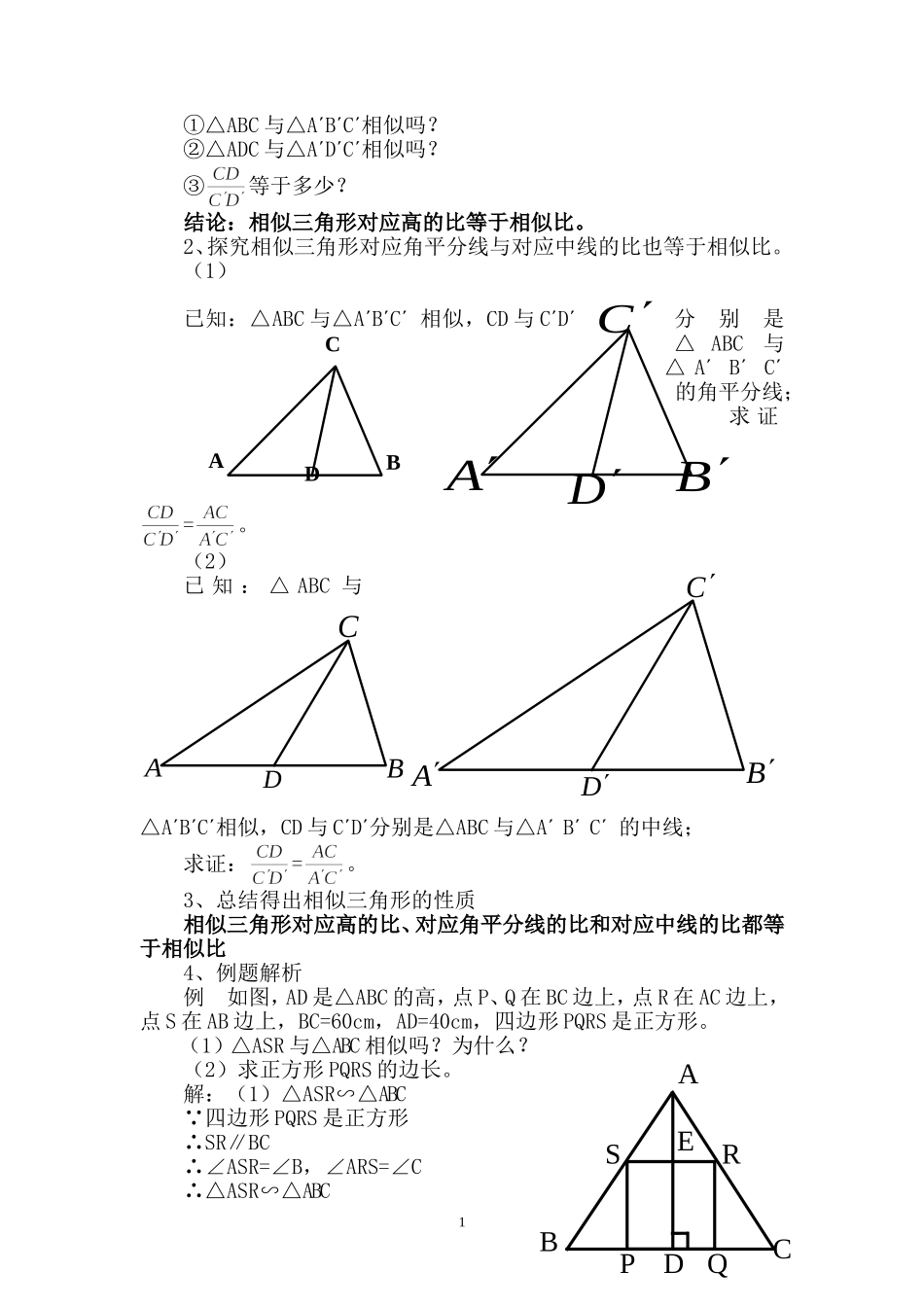
课题§4.8相似多边形的性质(1)【教学目标】一、知识与技能1.相似三角形的性质;2.用相似三角形的性质解决简单问题。二、过程与方法1.经历探索相似三角形中对应线段比值与相似比的关系的过程,理解相似三角形的性质;2.利用相似三角形的性质解决一些实际问题。三、情感态度与价值观1.通过探索相似三角形中对应线段的比与相似比的关系,培养学生的探索精神和合作意识;2.通过运用相似三角形的性质,增强学生的应用意识。【教学重点】1.相似三角形中对应线段比值的推导;2.运用相似三角形的性质解决实际问题。【教学难点】相似三角形性质的运用【教学关键】相似三角形性质的运用【教学方法】启发式【教学过程】一、复习1、相似三角形的定义及相关概念;2、相似三角形的判定方法。二、引入新课以P146页制作零件的问题引入新课。三、教授新课1、通过实例探索相似三角形对应高的比等于相似比;ABCDABCDABCD①△ABC与△A΄B΄C΄相似吗?②△ADC与△A΄D΄C΄相似吗?③等于多少?结论:相似三角形对应高的比等于相似比。2、探究相似三角形对应角平分线与对应中线的比也等于相似比。(1)已知:△ABC与△A΄B΄C΄相似,CD与C΄D΄分别是△ABC与△A΄B΄C΄的角平分线;求证=。(2)已知:△ABC与△A΄B΄C΄相似,CD与C΄D΄分别是△ABC与△A΄B΄C΄的中线;求证:=。3、总结得出相似三角形的性质相似三角形对应高的比、对应角平分线的比和对应中线的比都等于相似比4、例题解析例如图,AD是△ABC的高,点P、Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm,AD=40cm,四边形PQRS是正方形。(1)△ASR与△ABC相似吗?为什么?(2)求正方形PQRS的边长。解:(1)△ASR∽△ABC∵四边形PQRS是正方形∴SR∥BC∴∠ASR=∠B,∠ARS=∠C∴△ASR∽△ABC1ABCDABCSREPDQABCDABDC(2)由(1)可知△ASR∽△ABC,根据相似三角形对应高的比等于相似比,可得:设正方形PQRS的边长为xcm,则AE=(40-x)cm,所以解得x=24所以,正方形PQRS的边长为24cm四、随堂练习P148页知识技能1、2(备选)五、课堂小结1、相似三角形的性质及作用;2、用代数的方法解决几何问题。六、布置作业1、P148页习题4.10第3题2、P148页知识4.10第2题(备选)七、板书设计§4.8相似多边形的性质(1)2相似三角形的性质例题解析探究性质