初二数学《勾股定理》PPT课件VIP免费

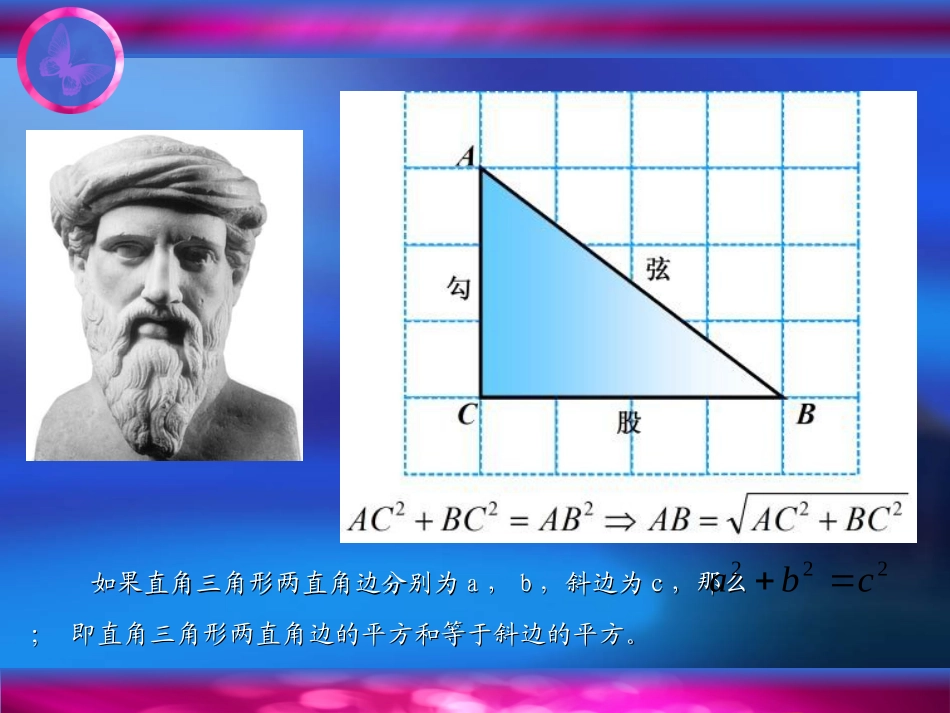
LOGO第十八章勾股定理第十八章勾股定理如果直角三角形两直角边分别为如果直角三角形两直角边分别为aa，，bb，斜边为，斜边为cc，那么，那么；即直角三角形两直角边的平方和等于斜边的平方。；即直角三角形两直角边的平方和等于斜边的平方。222cba勾股定理的证明勾股定理的证明证明方法证明方法11：数方格：数方格（（11）观察图）观察图1-11-1正方形正方形AA中含有中含有个小方格，即个小方格，即AA的面积是的面积是个单位面积。个单位面积。正方形正方形BB的面积是的面积是个单位面积。个单位面积。正方形正方形CC的面积是的面积是个单位面积。个单位面积。1616925你是怎样得到正方形c的面积。ABC图1-1（图中每个小方格代表一个单位面积）（图中每个小方格代表一个单位面积）（（22）在图）在图1-21-2中，正中，正方形方形AA，，BB，，CC中各含有多中各含有多少个小方格？它们的面积各少个小方格？它们的面积各是多少？是多少？（（33）你能发现图）你能发现图1-11-1中三个正方形中三个正方形AA，，BB，，CC的的面积之间有什么关系吗？图面积之间有什么关系吗？图1-21-2中呢？中呢？SA+SB=SCSA+SB=SC即：两条直角边上的正方形面积之和等于斜即：两条直角边上的正方形面积之和等于斜边上的正方形的面积边上的正方形的面积即：两条直角边上的正方形面积之和等于斜即：两条直角边上的正方形面积之和等于斜边上的正方形的面积边上的正方形的面积ABC图1-1ABC图1-2（（33）分别以）分别以55厘米、厘米、1212厘米为直角边作出一个直角三厘米为直角边作出一个直角三角形，并测量斜边的长度角形，并测量斜边的长度,,（（22）中的规律对这个三角形仍然）中的规律对这个三角形仍然成立吗？成立吗？（（11）你能用三角形）你能用三角形的边长表示正方形的面积吗？的边长表示正方形的面积吗？（（22）你能发现直角三）你能发现直角三角形三边长度之间存在什么角形三边长度之间存在什么关系吗？与同伴进行交流。关系吗？与同伴进行交流。直角三角形两直角边直角三角形两直角边的平方和等于斜边的平方的平方和等于斜边的平方ABC图1-1ABC图1-2勾股定理的证明勾股定理的证明证明方法证明方法22：拼三角形：拼三角形同学们动手一起拼同学们动手一起拼利用拼图来验证勾股定理：利用拼图来验证勾股定理：cab11、准备四个全等的直角三角形（设直角三、准备四个全等的直角三角形（设直角三角形的两条直角边分别为角形的两条直角边分别为aa，，bb，斜边为，斜边为cc）；）；22、你能用这四个直角三角形拼成一个以斜、你能用这四个直角三角形拼成一个以斜边边cc正方形吗？拼一拼试试看正方形吗？拼一拼试试看?3.3.你能否就你拼出的图说明你能否就你拼出的图说明aa22+b+b22=c=c22？？cabcabcabcabcab cc22=4•ab/2+(b-a)=4•ab/2+(b-a)22=2ab+b=2ab+b22-2ab+a-2ab+a22=a=a22+b+b22∴∴aa22+b+b22=c=c22大正方形的面积可以表示为；大正方形的面积可以表示为；也可以表示为也可以表示为c24•ab/2-(b-a)2cabcabcabcab (a+b)2=c2+4•ab/2a2+2ab+b2=c2+2ab∴a2+b2=c2大正方形的面积可以表示为；大正方形的面积可以表示为；也可以表示为也可以表示为(a+b)2c2+4•ab/2勾股定理的证明勾股定理的证明证明方法证明方法33：赵爽弦图，动手拼图：赵爽弦图，动手拼图cabcab勾股定理的证明勾股定理的证明证明方法证明方法44：美国总统加菲尔德的证明方法：美国总统加菲尔德的证明方法在直角三角形中，已知两边可以求第三边在直角三角形中，已知两边可以求第三边例1如图，在Rt△ABC中,BC=24,AC=7,求AB的长。在Rt△ABC中,根据勾股定理222BCACAB解：B24AC76252472225AB如果将题目变为：在Rt△ABC中,AB=25,BC=24,求AC的长呢？2524例2已知等边三角形ABC的边长是6cm，(1)求高AD的长；(2)S△ABCABCD解：(1) △ABC是等边三角形，AD是高在Rt△ABD中,根据勾股定理222BDABADcmAD3327936ADBCSABC21)2()(39336212cm321BCBD例3如图，∠ACB=∠ABD=90°，CA=CB，∠DAB=30°，AD=8，求AC的长。解： ∠ABD=90°，∠DAB=30°∴BD=AD=421在Rt△ABD中,根据勾股定理484822222...