双曲线的简单几何性质VIP免费

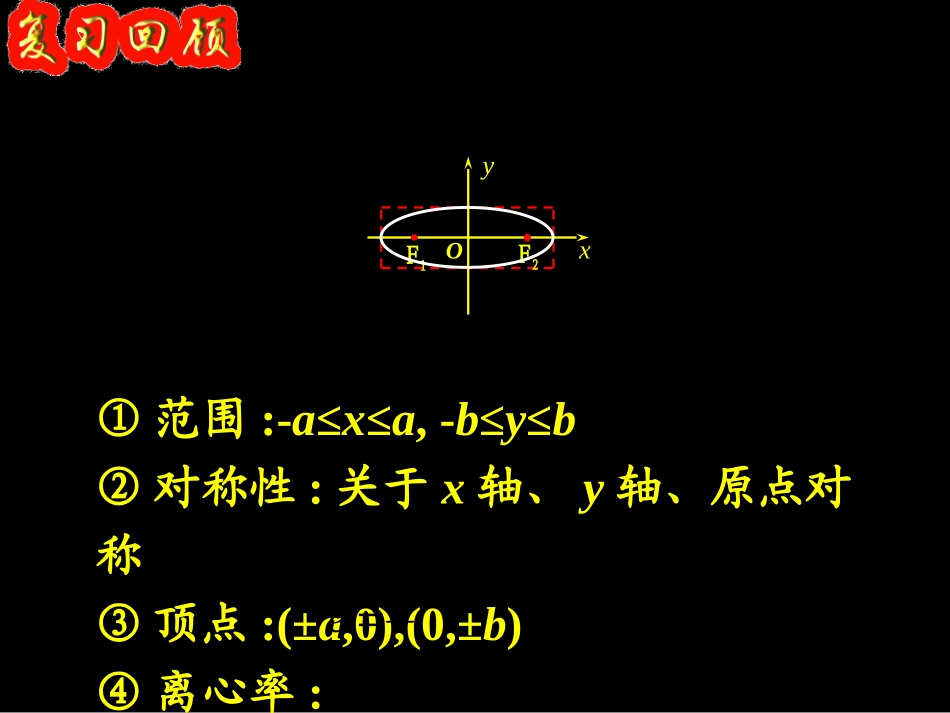
xyOF2F1xyOF2F112222byax12222bxay①范围:-a≤x≤a,-b≤y≤b②对称性:关于x轴、y轴、原点对称③顶点:(±a,0),(0,±b)④离心率:ace12222byaxyxOF2F12、对称性研究双曲线的简单几何性质1、范围关于x轴、y轴和原点都是对称的.x轴、y轴是双曲线的对称轴，原点是对称中心，又叫做双曲线的中心。xyo-aa(-x,-y)(-x,y)(x,y)(x,-y))0,0(12222babyaxax,axax,1ax2222即研究双曲线的简单几何性质xyo)0,0(12222babyax3、顶点（1）双曲线与对称轴的交点，叫做双曲线的顶点-b1B2Bb1A2A如图，线段A1A2叫做双曲线的实轴，它的长为2a,a叫做半实轴长；线段B1B2叫做双曲线的虚轴，它的长为2b,b叫做双曲线的半虚轴长.（2）顶点是A1(-a,0)、A2(a,0)-aa研究双曲线的简单几何性质)0,0(12222babyax4、渐近线byxa直线叫做双曲线的渐进线.xyOxabyxaby研究双曲线的简单几何性质)0,0(12222babyax4、渐近线22byxaa22||1baxax221baxaxx当时,220.ax,xbyxa说明:当时双曲线上点的纵坐标与的纵坐标很接近.21121,.babyxyxxyyaxa即与中，当时xyOxabyxaby研究双曲线的简单几何性质)0,0(12222babyax4、渐近线byxa直线叫做双曲线的渐进线.的渐进线为：13422yxxy23的渐进线为：12222yxxyxyOxabyxaby(0)bxyyxaab令中的1为0,再化简所得的直线方程.22221xyab研究双曲线的简单几何性质)0,0(12222babyax5、离心率双曲线的叫做的比双曲线的焦距与实轴长,ace离心率。c>a>0e>1e是表示双曲线开口大小的一个量,e越大开口越大!（1）定义：（2）e的范围：（3）e的含义：2221()cabbeaaa也增大增大且时，当ab,e),,0(ab),1(e的夹角增大增大时，渐近线与实轴e研究双曲线的简单几何性质)0,0(12222babyax等轴双曲线:实轴和虚轴等长的双曲线——等轴双曲线.等轴双曲线的离心率为——2等轴双曲线的两渐近线为y=±x,互相垂直(所成角为90°).双曲线的两条渐近线互相垂直,那么该双曲线的离心率是A.2B.C.D.233212222byax)0(22mmyx例求双曲线9y2-16x2=144的半实轴长和半虚轴长、焦点坐标、离心率、渐近线方程.例题剖析xyO标准方程焦点坐标图形12222byax12222bxayxyO(-c,0)和(c,0)(0,-c)和(0,c)范围对称性顶点x≥a或x≤-ay≥a或y≤-a坐标轴是对称轴;原点是对称中心,叫双曲线的中心.A1(-a,0)和A2(a,0)A1A2叫实轴,B1B2叫虚轴,且|A1A2|=2a,|B1B2|=2bF2A1(0,-a)和A2(0,a)渐近线xabyyabx离心率e=ac（e>1,且e决定双曲线的开口程度,越大开口越阔）F1F2F1A2A1B1B2B1B2A2A1