圆周角定理的应用MicrosoftPowerPoint演示文稿VIP免费

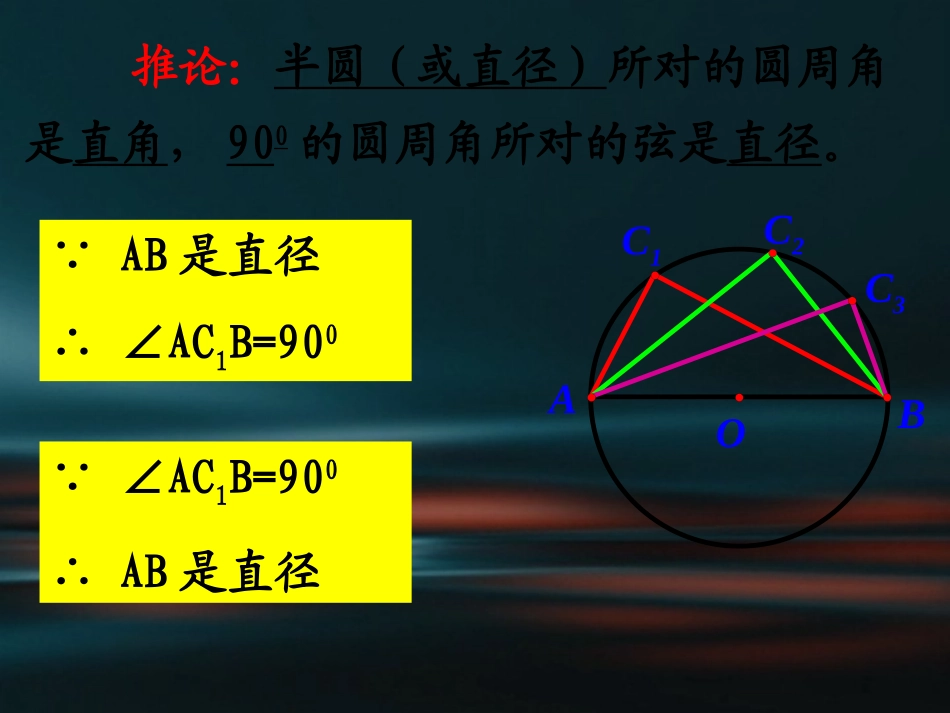
九年级数学上册（人教版）24.1.4（2）圆周角定理的应用康平二中顾大力在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．圆周角定理·CDABO老师提示:圆周角定理是承上启下的知识点,要予以重视.推论：半圆（或直径）所对的圆周角是直角，900的圆周角所对的弦是直径。AOBC1C2C3∵AB是直径∴∠AC1B=900∵∠AC1B=900∴AB是直径同圆或等圆中，相等的圆周角所对的弧也相等。DABOCEFF∵∠CAD=∠EBF∴CD=EF））课前练习：1.如图，等边三角形ABC，点D是⊙O上一点，则∠BDC=；图3ODCBA60°2.如图，在⊙O中，AB是⊙O的直径，∠D＝20°，则∠AOC的度数为_____140°ABDCO3.如图，AB和CD都是⊙0的直径，∠AOC=60°，则∠C的度数是。30°5.如图,∠C是⊙O的圆周角，∠C=38°，则∠OAB=.CBＡＯ4、如图，AB是⊙O的直径，点C在圆上，∠A=20°,则∠B=度6.如图，在⊙O中，∠AOD=120º，∠BDP=25º，则∠P的度数等于。70°52°35°教学目标：1、理解并运用圆周角定理及其推论2、掌握圆的内接四边形的性质3、通过引导学生添加合理的辅助线，培养学生的创造能力•教学重点：•圆周角定理及其推论•教学难点：•圆周角定理及其推论的运用新课讲解：若一个多边形各顶点都在同一个圆上，那么，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆。OBCDEFAOACDEBOCABD如图，四边形ABCD为⊙O的内接四边形；⊙O为四边形ABCD的外接圆。CODBA如图：圆内接四边形ABCD中，∵弧BCD和弧BAD所对的圆心角的和是周角∴∠A＋∠C＝180°同理∠B＋∠D＝180°圆的内接四边形的对角互补。例1、在⊙O中，∠CBD=30°，∠BDC=20°,求∠A。OABDC解：∵∠CBD=300，∠BDC=200∴∠C=1800-∠CBD-∠BDC=1300∴∠A=1800-∠C=500（圆内接四边形对角互补）变式：已知∠OAB等于40度,求∠C的度数.ABCOD例2、如图，在⊙O中，AB为直径，CB=CF,弦CG⊥AB，交AB于D，交BF于E。求证：BE=EC））OABDCEGFBE=EC∠EBC=∠ECBCF=BG））CB=BG））CB=CF））AB为直径CG⊥AB1、填空(1)四边形ABCD内接于⊙O，则∠A+∠C=__，∠B+∠ADC=_____;若∠B=800，则∠ADC=______∠CDE=______(2)四边形ABCD内接于⊙O，∠AOC=1000则∠B=______∠D=______(3)四边形ABCD内接于⊙O,∠A:∠C=1:3,则∠A=_____,EDBAC80DBACO100180°180°100°80°50°130°45°巩固练习2、选择：若ABCD为圆内接四边形，则下列哪个选项可能成立（）（A）∠ABCD∶∠∶∠∶∠＝123∶∶4∶（B）∠ABCD∶∠∶∠∶∠＝213∶∶4∶（C）∠ABCD∶∠∶∠∶∠＝321∶∶4∶（D）∠ABCD∶∠∶∠∶∠＝4321∶∶∶B3、判断（打“√”或“×”)1.同弧或等弧所对的圆周角相等.()2.相等的圆周角所对的弧相等.()3.90°角所对的弦是直径.()4.直径所对的角等于90°.()5.长等于半径的弦所对的圆周角等于30°.()√××××44、、已知：如图，在△ABC中，AB=AC,以AB为直径的圆交BC于D,交AC于E,(1)BD与CD的大小有什么关系?为什么?(2)求证：⌒⌒BD=DE连结AD.∵AB是圆的直径，点D在圆上，∴∠ADB=90°，∴ADBC⊥，∵AB=AC，∴BD=CD,AD平分顶角∠BAC，即∠BAD=CAD∠，∴⌒⌒BD=DE（同圆或等圆中相等的圆周角所对弧相等）。ABCDE解:BD=CD.理由是:5、如图，⊙O直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC、AD、BD的长．86102222ACABBC又在Rt△ABD中，AD2+BD2=AB2，221052(cm)22ADBDAB解：∵AB是直径，∴∠ACB=∠ADB=90°．在Rt△ABC中，∵CD平分∠ACB，∴AD=BD..ACDBCDOABCD6、求证：如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形．（提示：作出以这条边为直径的圆.）·ABCO求证：△ABC为直角三角形.证明：CO=AB,12以AB为直径作⊙O，∵AO=BO，∴AO=BO=CO.∴点C在⊙O上.又∵AB为直径,∴∠ACB=×180°=90°.12已知：△ABC中，CO为AB边上的中线，12且CO=AB∴△ABC为直角三角形.小结1、本节课我们学习了哪些知识？（1）圆周角定理及推论的应用（2）圆的内接四边形性质定理2、本节课我们学习了哪些引辅助线的方法？（1）构造直径上的圆周角（2）构造同弧或等弧所对的圆周角作业•习题：24.1第10、11题结束寄语•要养成用数学的语言去说明道理,用数学的思维去解读世界的习惯.下课了!