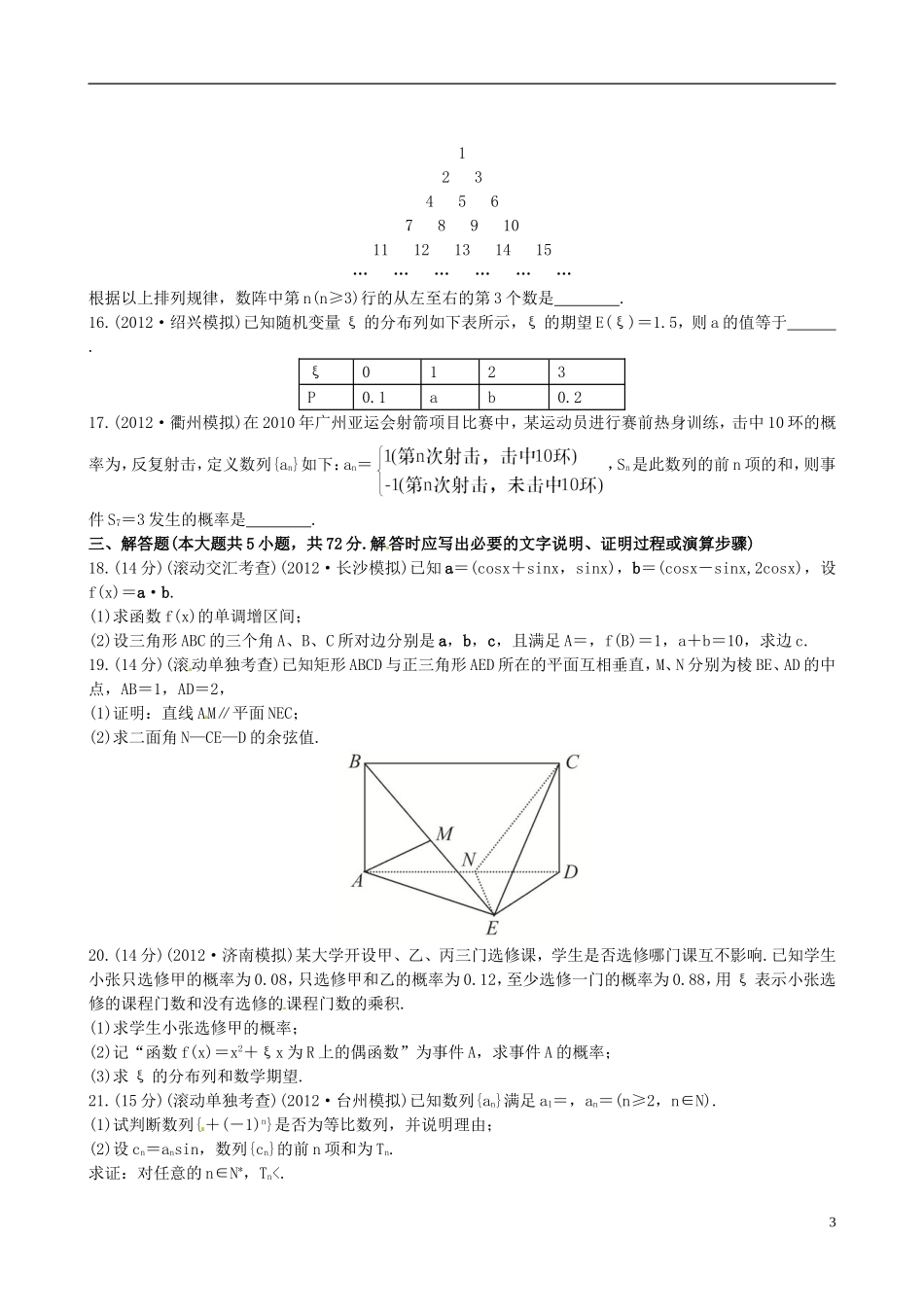
【全程复习方略】(浙江专用)2013版高考数学阶段滚动检测(六)理新人教A版(120分钟150分)第Ⅰ卷(选择题共50分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(滚动单独考查)设全集U=R,集合A={x|2x(x-2)<1},B={x|y=ln(1-x)},则图中阴影部分表示的集合为()(A){x|x≥1}(B){x|x≤1}(C){x|03,n∈N*)维向量.n维向量可用(x1,x2,x3,x4,…,xn)表示.设a=(a1,a2,a3,a4,…,an),b=(b1,b2,b3,b4,…,bn),a与b夹角θ的余弦值为cosθ=.当两个n维向量a=(1,1,1,1,…,1),b=(-1,-1,1,1,…,1)时,cosθ=.15.将全体正整数排成一个三角形数阵:2123456789101112131415………………根据以上排列规律,数阵中第n(n≥3)行的从左至右的第3个数是.16.(2012·绍兴模拟)已知随机变量ξ的分布列如下表所示,ξ的期望E(ξ)=1.5,则a的值等于.ξ0123P0.1ab0.217.(2012·衢州模拟)在2010年广州亚运会射箭项目比赛中,某运动员进行赛前热身训练,击中10环的概率为,反复射击,定义数列{an}如下:an=,Sn是此数列的前n项的和,则事件S7=3发生的概率是.三、解答题(本大题共5小题,共72分.解答时应写出必要的文字说明、证明过程或演算步骤)18.(14分)(滚动交汇考查)(2012·长沙模拟)已知a=(cosx+sinx,sinx),b=(cosx-sinx,2cosx),设f(x)=a·b.(1)求函数f(x)的单调增区间;(2)设三角形ABC的三个角A、B、C所对边分别是a,b,c,且满足A=,f(B)=1,a+b=10,求边c.19.(14分)(滚动单独考查)已知矩形ABCD与正三角形AED所在的平面互相垂直,M、N分别为棱BE、AD的中点,AB=1,AD=2,(1)证明:直线AM∥平面NEC;(2)求二面角N—CE—D的余弦值.20.(14分)(2012·济南模拟)某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响.已知学生小张只选修甲的概率为0.08,只选修甲和乙的概率为0.12,至少选修一门的概率为...