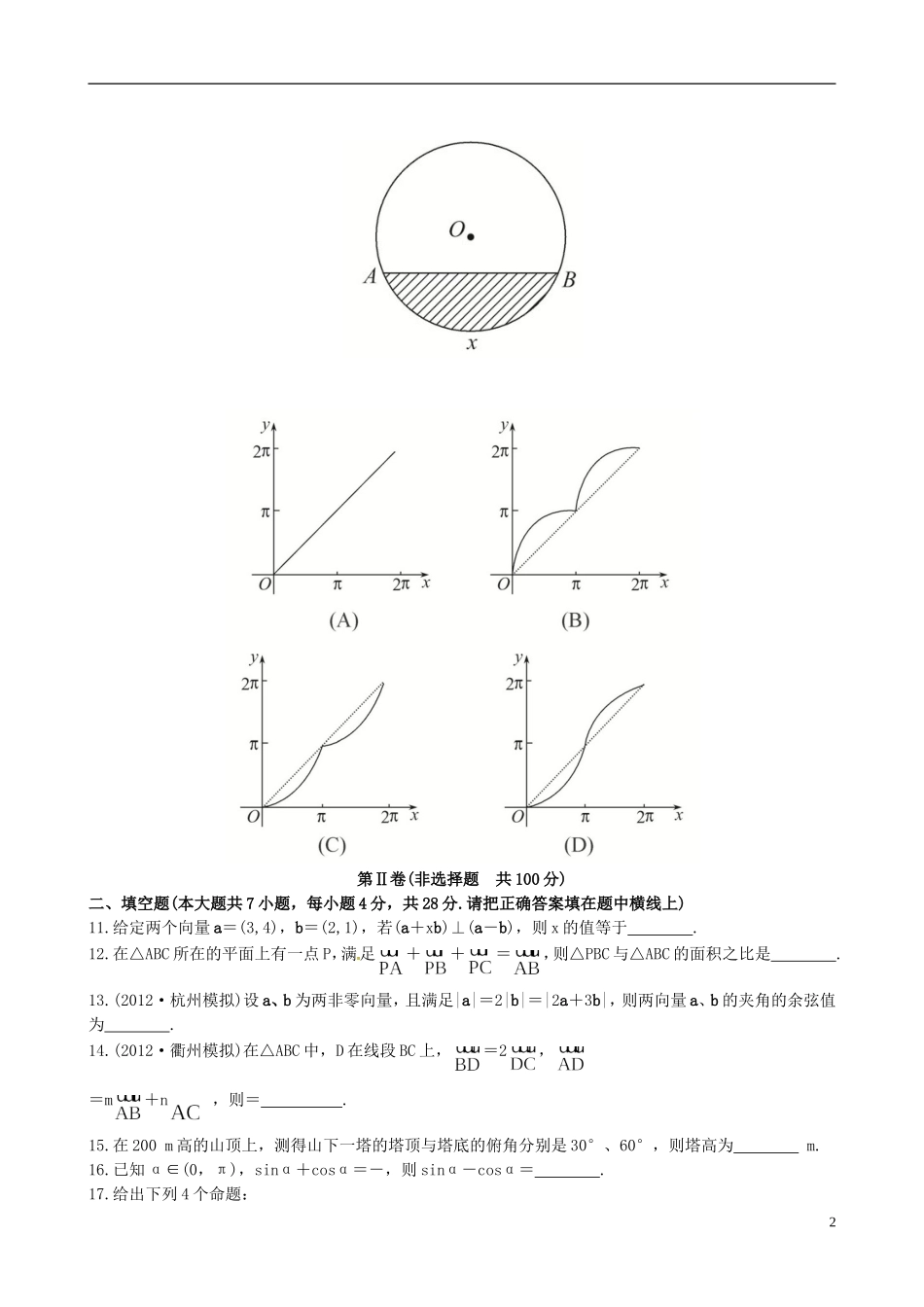
【全程复习方略】(浙江专用)2013版高考数学阶段滚动检测(二)理新人教A版(120分钟150分)第Ⅰ卷(选择题共50分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.集合A={y∈R|y=2x},B={-1,0,1},则下列结论正确的是()(A)A∩B={0,1}(B)A∪B=(0,+∞)(C)(RA)∪B=(-∞,0)(D)(RA)∩B={-1,0}2.(2012·宁波模拟)()2010+()2011+()2012+()2013=()(A)0(B)i(C)-i(D)13.若=(1,1),=(3,8),=(0,1),+=(a,b),则a+b=()(A)-1(B)0(C)1(D)24.过原点和复数1-i在复平面内对应点P的直线OP的倾斜角为()(A)-(B)(C)(D)5.已知tanα=-,则的值是()(A)(B)-(C)(D)-6.(滚动单独考查)已知f()=,则f(x)的解析式为()(A)f(x)=(B)f(x)=-(C)f(x)=(D)f(x)=-7.(2012·温州模拟)若平面向量b与向量a=(2,1)平行,且|b|=2,则b=()(A)(4,2)(B)(-4,-2)(C)(6,-3)(D)(4,2)或(-4,-2)8.已知点O(0,0),A(2,1),B(-1,7),=+,又⊥,且||=2,则Q点的坐标为()(A)(,)或(-,-)(B)(,)(C)(-,-)(D)(,)或(,)9.函数y=sin(2x+)图象的对称轴方程可能是()(A)x=-(B)x=-(C)x=(D)x=10.(滚动单独考查)如图所示,单位圆中弧的长为x,f(x)表示弧与弦AB所围成弓形的面积的2倍,则函数y=f(x)的图象是()1第Ⅱ卷(非选择题共100分)二、填空题(本大题共7小题,每小题4分,共28分.请把正确答案填在题中横线上)11.给定两个向量a=(3,4),b=(2,1),若(a+xb)⊥(a-b),则x的值等于.12.在△ABC所在的平面上有一点P,满足++=,则△PBC与△ABC的面积之比是.13.(2012·杭州模拟)设a、b为两非零向量,且满足|a|=2|b|=|2a+3b|,则两向量a、b的夹角的余弦值为.14.(2012·衢州模拟)在△ABC中,D在线段BC上,=2,=m+n,则=.15.在200m高的山顶上,测得山下一塔的塔顶与塔底的俯角分别是30°、60°,则塔高为m.16.已知α∈(0,π),sinα+cosα=-,则sinα-cosα=.17.给出下列4个命题:2①非零向量a,b满足|a|=|b|=|a-b|,则a与a+b的夹角为30°;②“a·b>0”是“a,b的夹角为锐角”的充要条件;③将函数y=|x+1|的图象按向量a=(-1,0)平移,得到的图象对应的函数表达式为y=|x+2|;④在△ABC中,若(+)·(-)=0,则△ABC为等腰三角形.其中正确的命题是.(注:把你认为正确的命题的序号都填上)三、解答题(本大题共5小题,共72分.解答时应写出必要的文字说明、证明过程或演算步骤)18.(14分)(2012·杭州模拟)已知a=(2,cosx),b=(sin(x+),-2),函数f(x)=a·b(x∈R).(1)求函数f(x)的单调增区间;(2)若f(x)=,求cos(2x-)的值.19.(14分)(2012·哈尔滨模拟)在四边形ABCD中,||=12,||=5,||=10,|+|=||,在方向上的投影为8.(1)求∠BAD的正弦值;(2)求△BCD的面积.20.(14分)(2012·郑州模拟)在锐角△ABC中,已知内角A、B、C所对的边分别为a、b、c,且满足2sinB(2cos2-1)=-cos2B.(1)求B的大小;(2)如果b=2,求△ABC的面积S△ABC的最大值.21.(15分)已知点F(1,0),点P在y轴上运动,点M在x轴上运动,设P(0,b),M(a,0)且·=0,动点N满足2+=0.(1)求点N的轨迹C的方程;(2)F′为曲线C的准线与x轴的交点,过点F′的直线l交曲线C于不同的两点A、B,若D为AB的中点,在x轴上存在一点E,使·(-)=0,求||的取值范围(O为坐标原点).22.(15分)(2012·西安模拟)函数f(x)=x3-(a+1)x+a,g(x)=xlnx.(1)若y=f(x),y=g(x)在x=1处的切线相互垂直,求这两个切线方程;(2)若F(x)=f(x)-g(x)在定义域上单调递增,求a的取值范围.答案解析1.【解析】选D.因为A={y∈R|y=2x}={y|y>0},RA={y|y≤0},∴(RA)∩B={-1,0}.2.【解析】选A.原式=i2010+i2011+i2012+i2013=i4×502+2+i4×502+3+i4×503+i4×503+1=i2+i3+1+i=-1-i+1+i=0.3.【解析】选A. +==-=(-1,0),∴a=-1,b=0,∴a+b=-1.4.【解析】选C.设倾斜角为α,如图所示,3易知α=.5.【解析】选C.tanα=-,则tan2α=-,原式==.6.【解析】选C.(特殊值法):对于f()=,令x=0,代入其中有f(1)=1.经检验只有选项C满足f(1)...