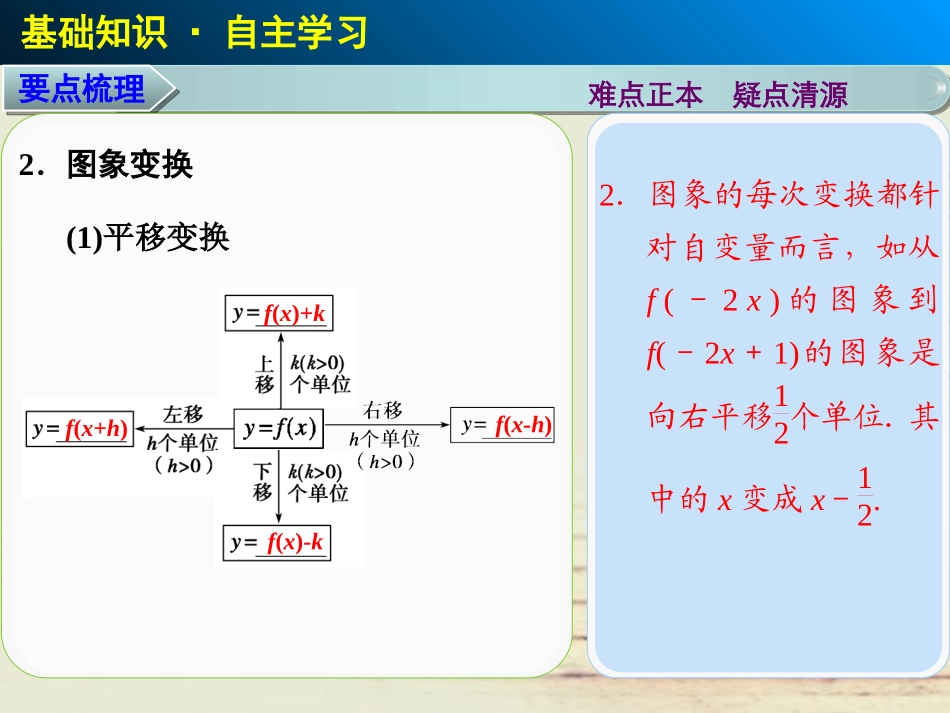
§2.9§2.9函数的图象数学苏(理)第二章函数与基本初等函数Ⅰ基础知识·自主学习难点正本疑点清源要点梳理1.数形结合的思想方法是学习函数内容的一条主线,也是高考考查的热点.作函数图象首先要明确函数图象的形状和位置.1.描点法作图方法步骤:(1)确定函数的定义域;(2)化简函数的解析式;(3)讨论函数的性质即奇偶性、周期性、单调性、最值(甚至变化趋势);(4)描点连线,画出函数的图象.基础知识·自主学习难点正本疑点清源要点梳理2.图象的每次变换都针对自变量而言,如从f(-2x)的图象到f(-2x+1)的图象是向右平移12个单位.其中的x变成x-12.2.图象变换(1)平移变换f(x)+kf(x-h)f(x)-kf(x+h)基础知识·自主学习难点正本疑点清源要点梳理(2)对称变换①y=f(x)―――――→关于x轴对称y=;②y=f(x)―――――→关于y轴对称y=;③y=f(x)―――――→关于原点对称y=;④y=ax(a>0且a≠1)―――――→关于y=x对称y=.(3)翻折变换①y=f(x)―――――――――→保留x轴上方图象将x轴下方图象翻折上去y=.②y=f(x)――――――――――→保留y轴右边图象,并作其关于y轴对称的图象y=.-f(x)f(-x)-f(-x)logax(a>0且a≠1)|f(x)|f(|x|)2.图象的每次变换都针对自变量而言,如从f(-2x)的图象到f(-2x+1)的图象是向右平移12个单位.其中的x变成x-12.基础知识·自主学习难点正本疑点清源要点梳理3.要理解一个函数的图象自身的对称性和两个不同函数图象对称关系的不同.(4)伸缩变换①y=f(x)y=.②y=f(x)y=.f(ax)af(x)题号答案解析12345基础知识·自主学习基础自测右1(-2,0)∪(2,5]y=(x-1)2+321-22,3【例1】分别画出下列函数的图象:(1)y=|lgx|;(2)y=2x+2;(3)y=x2-2|x|-1;(4)y=x+2x-1.题型分类·深度剖析题型一作函数图象思维启迪解析探究提高基础知识题型分类思想方法练出高分题型分类·深度剖析根据一些常见函数的图象,通过平移、对称等变换可以作出函数图象.思维启迪解析探究提高题型一作函数图象【例1】分别画出下列函数的图象:(1)y=|lgx|;(2)y=2x+2;(3)y=x2-2|x|-1;(4)y=x+2x-1.基础知识题型分类思想方法练出高分【例1】分别画出下列函数的图象:(1)y=|lgx|;(2)y=2x+2;(3)y=x2-2|x|-1;(4)y=x+2x-1.题型分类·深度剖析思维启迪解析探究提高题型一作函数图象解(1)y=lgxx≥1,-lgx0