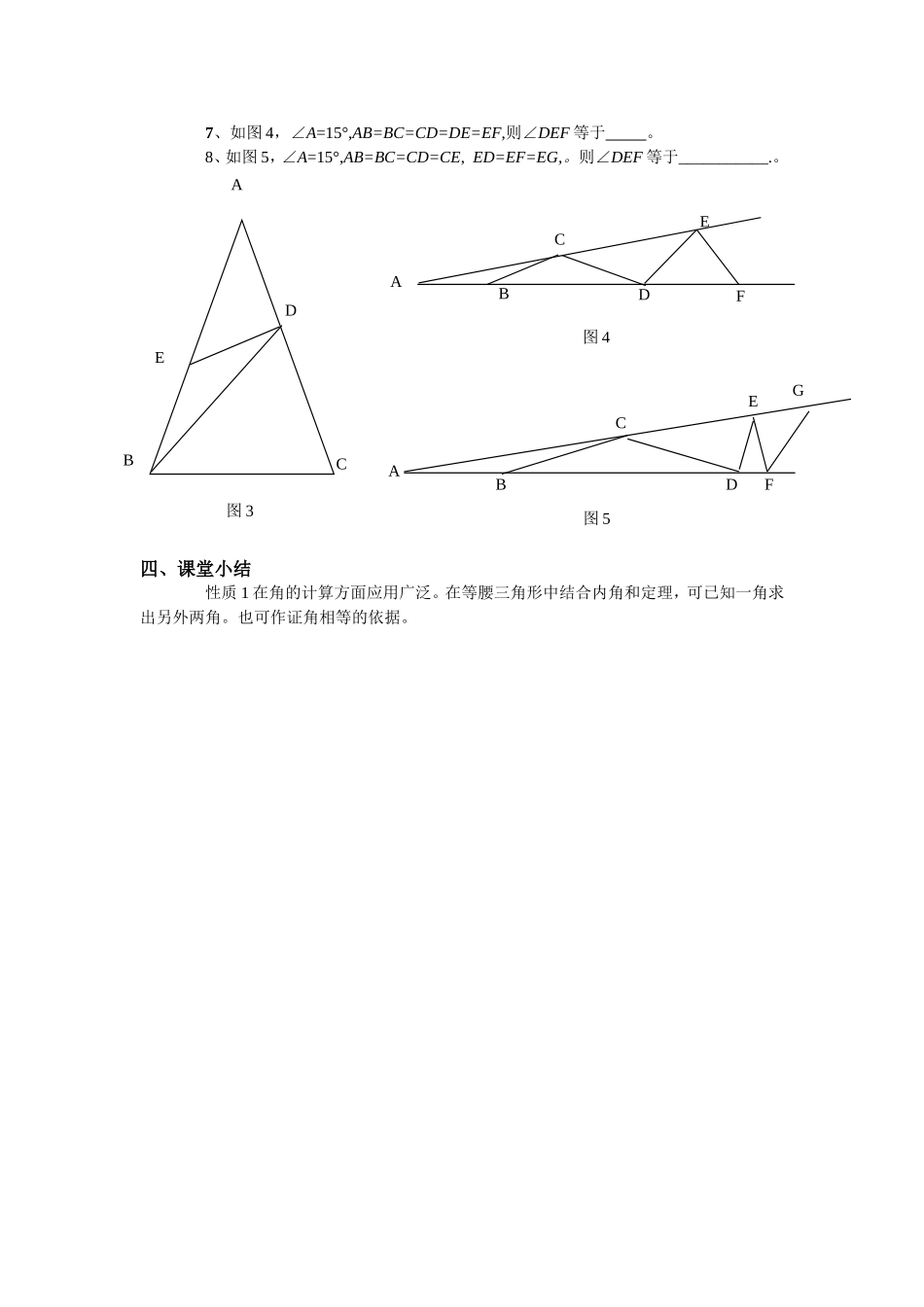
等腰三角形的性质(1)曹市庆丰中学郭成军教学目标1.经历等腰三角形的得出过程,从轴对称的角度体会其特点。2.探索并掌握等腰三角形的性质。3.通过学生的操作和思考,使学生掌握等腰三角形的相关概念,并在探究等腰三角形性质的过程中培养学生认真思考的习惯。重点难点重点:1等腰三角形的概念及性质。2等腰三角形性质的应用。难点:等腰三角形性质的理解及应用。教学过程一、剪一剪问题1:拿出事先准备好的长方形纸片,试剪出一个等腰三角形。问题2:△ABC有什么特点?结合学生回答给出等腰三角形及其相关概念。问题3:△ABC是轴对称图形吗?它的对称轴是什么?二、证一证问题1:通过上面的操作,你发现了什么现象,猜想等腰△ABC有那些性质?学生讨论、汇报∠B=∠C——两个底角相等用语言叙述为:性质1:等腰三角形的两个底角相等(简写成等边对等角)。问题2:你能用所学知识验证等腰三角形的性质吗?如图1,在△ABC中,AB=AC。求证:∠B=∠C三、用一用。例题1:如图2,在△ABC中AB=AC,且BD=BC=AD,求△ABC各角的度数。随堂练习1、等腰三角形底角为30°,则这个等腰三角形各角度数为。2、等腰三角形一角为30°,则这个等腰三角形各角度数为。3、等腰三角形一角为150°,则这个等腰三角形各角度数为。4、等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的顶角为。5、如图3,在△ABC中,AB=AC,BC=BD,AD=DE=EB,则∠A=。6、等腰三角形被过一个顶点的一条直线分割成两个较小的等腰三角形,请你画出所有符合条件的三角形的草图.ACDB图2ACB图17、如图4,∠A=15°,AB=BC=CD=DE=EF,则∠DEF等于。8、如图5,∠A=15°,AB=BC=CD=CE,ED=EF=EG,。则∠DEF等于___________.。四、课堂小结性质1在角的计算方面应用广泛。在等腰三角形中结合内角和定理,可已知一角求出另外两角。也可作证角相等的依据。ABCDEE图3ABCDF图4ABCDEFG图5