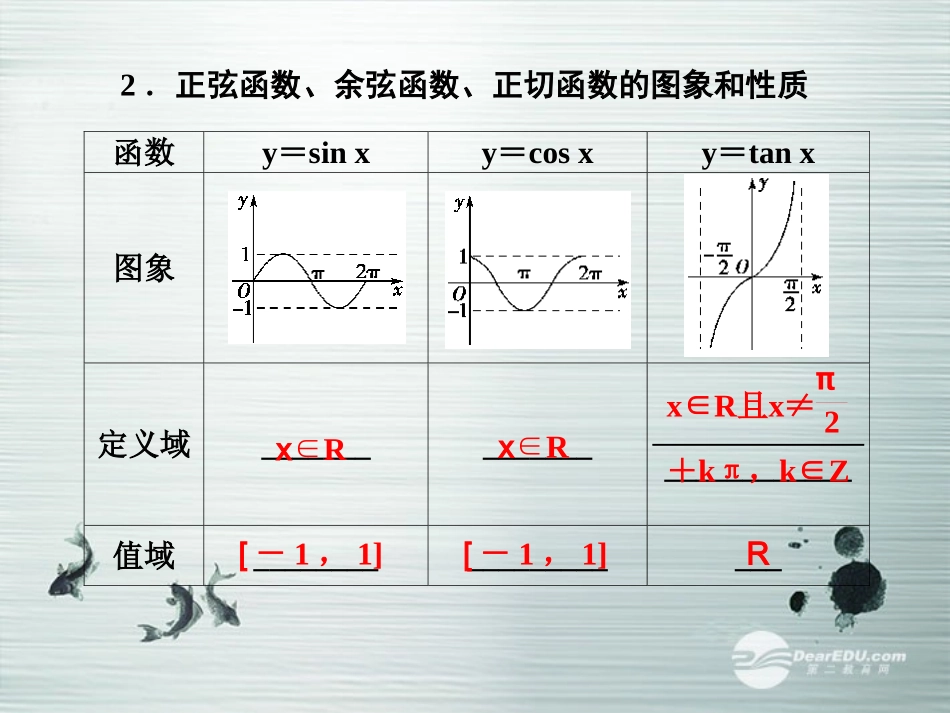
第三节三角函数的图象与性质1.周期函数和最小正周期对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有____________,则称f(x)为周期函数,T为它的一个周期.若在所有周期中,有一个_____的正数,则这个最小的正数叫做f(x)的_____________.f(x+T)=f(x)最小最小正周期2.正弦函数、余弦函数、正切函数的图象和性质函数y=sinxy=cosxy=tanx图象定义域__________________________值域____________________xR∈xR∈x∈R且x≠π2+kπ,k∈Z[-1,1][-1,1]R单调性递增区间是_________(k∈Z),递减区间是________________________(k∈Z)递增区间是___________(k∈Z),递减区间是______(k∈Z)递增区间是____________(k∈Z)[2kπ-π2,2kπ+π2][2kπ+π2,2kπ+3π2][2kπ-π,2kπ][2kπ,2kπ+π](kπ-π2,kπ+π2)最值ymax=1;ymin=-1ymax=1;ymin=___无最大值和最小值奇偶性奇函数偶函数奇函数对称中心_________(kπ+π2,0),k∈Z________对称性对称轴x=kπ+π2,k∈Z________无对称轴最小正周期2π2ππ-1(kπ,0),k∈Z(kπ2,0),k∈Zx=kπ,kZ∈1.是否每一个周期函数都有最小正周期?【提示】不一定.如常数函数f(x)=a,每一个非零数都是它的周期.2.正弦函数和余弦函数的图象的对称轴及对称中心与函数图象的关键点是什么关系?【提示】y=sinx与y=cosx的对称轴方程中的x都是它们取得最大值或最小值时相应的x.对称中心的横坐标都是它们的零点.1.(人教A版教材习题改编)函数y=tan3x的定义域为()A.{x|x≠32π+3kπ,k∈Z}B.{x|x≠π6+kπ,k∈Z}C.{x|x≠-π6+kπ,k∈Z}D.{x|x≠π6+kπ3,k∈Z}【答案】D【解析】由3x≠π2+kπ,k∈Z得x≠π6+kπ3,k∈Z.2.函数f(x)=2cos(x+5π2)是()A.最小正周期为2π的奇函数B.最小正周期为2π的偶函数C.最小正周期为2π的非奇非偶函数D.最小正周期为π的偶函数【解析】f(x)=2cos(x+52π)=2cos(x+π2)=-2sinx,故f(x)是最小正周期为2π的奇函数.【答案】A3.(2012·福建高考)函数f(x)=sin(x-π4)的图象的一条对称轴是()A.x=π4B.x=π2C.x=-π4D.x=-π2【解析】 正弦函数图象的对称轴过图象的最高(低)点,故令x-π4=kπ+π2,k∈Z,∴x=kπ+3π4,k∈Z.取k=-1,则x=-π4.【答案】C4.函数y=2-3cos(x+π4)的最大值为________,此时x=________.【解析】当cos(x+π4)=-1时,函数有最大值5,此时,x+π4=π+2kπ,k∈Z,即x=34π+2kπ,k∈Z.【答案】534π+2kπ,k∈Z(1)(2012·山东高考)函数y=2sin(πx6-π3)(0≤x≤9)的最大值与最小值之和为()A.2-3B.0C.-1D.-1-3(2)f(x)=1+log12x+tan(x+π4)的定义域是________.【思路点拨】(1)先确定πx6-π3的范围,再数形结合求最值;(2)转化为关于x的不等式组求解.【尝试解答】(1) 0≤x≤9,∴-π3≤π6x-π3≤7π6,∴sin(π6x-π3)∈[-32,1].∴y∈[-3,2],∴ymax+ymin=2-3.(2)依题意1+log12x≥0,x+π4≠kπ+π2(k∈Z).∴0<x≤2,且x≠kπ+π4(k∈Z),∴函数f(x)的定义域是{x|0<x≤2,且x≠π4}.【答案】(1)A(2){x|0<x≤2,且x≠π4}(1)函数y=2sinx-1的定义域为________.(2)当x∈[π6,7π6]时,函数y=3-sinx-2cos2x的最小值是________,最大值是________.【解析】(1)由2sinx-1≥0得sinx≥12,∴2kπ+π6≤x≤2kπ+5π6,k∈Z,故函数的定义域为[2kπ+π6,2kπ+56π](k∈Z).(2)由π6≤x≤76π,知-12≤sinx≤1.又y=3-sinx-2cos2x=2sin2x-sinx+1=2(sinx-14)2+78,∴当sinx=14时,ymin=78,当sinx=1或-12时,ymax=2.【答案】(1)[2kπ+π6,2kπ+5π6](k∈Z)(2)782【思路点拨】(1)求定义域时考虑分母不为零,然后对f(x)解析式进行化简,转化成正弦型函数的形式,再求周期;(2)求单调递减区间时利用整体代换,把ωx+φ当作一个整体放入正弦的增区间内解出x即为增区间,不要忽略定义域.(2012·北京高考)已知函数f(x)=(sinx-cosx)sin2xsinx.(1)求f(x)的定义域及最小正周期;(2)求f(x)的单调递增区...