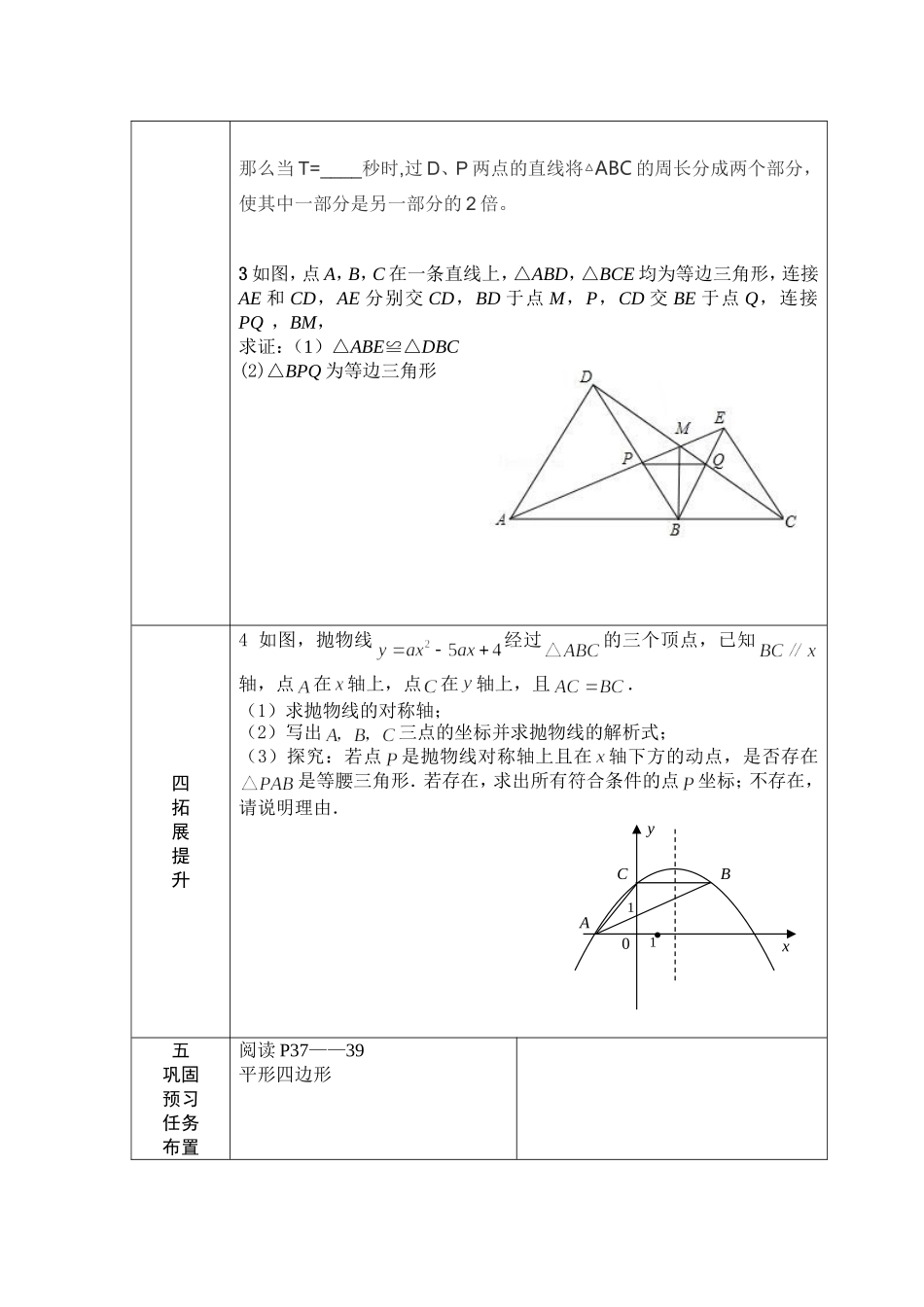
河田二中“五环节”课堂教学设计课题:等腰三角形复习第周第课时时间20164授课者:钟永秀教学目标:1、理解等腰三角形的2、掌握等腰三角形和等边三角形的性质和判定;并会运用它们解决有关的推理和计算问题。3、线段垂直平分线的性质与判定教学重难点:重点:等腰三角形和等边三角形的性质和判定难点:运用等腰三角形和等边三角形的性质和判定解决有关的推理和计算问题设计理念:先学后教讲练结合法讨论探究法预习回顾;1有一个等腰三角形的两条边长分别是4cm和8cm,则周长为_____(变式:两条边长分别是5cm和8cm)2等腰三角形的一个内角为100°,底角为_____(变式:①一个角为80°②一个外角为100°,则底角为_____.3如图,△ABC中,AB+AC=6cm,BC的垂直平分线l与AC相交于点D,则△ABD的周长为cm.4如图,已知△ABC是等边三角形,点B、C,D、E在同一直线上,且CG=CD,DF=DE,则∠E=_____教学流程环节学生活动教师活动一预习反馈回忆知识点1.等腰三角形的性质与判定:(1)等腰三角形的两底角__________;(2)等腰三角形底边上的高,底边上的_______,顶角的_______,互相重合(三线合一);(3)有的三角形是等腰三角形,有()的三角形是等腰三角形。2.等边三角形的性质与判定:(1)等边三角形每个角都等于_______,同样具画出草图帮助学生理解有关知识有“三线合一”的性质;(2)三个角相等的三角形是_______,三边相等的三角形是_,一个角等于60°的______三角形是等边三角形.3.轴对称性——线段垂直平分线的性质与判定:(1)线段垂直平分线上的点到_______的距离相等。(2)到线段两个端点的距离相等的点在这条线段的上二展示交流例1.如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于M,有下面4个结论:①射线BD是△ABC是角平分线;②图中共有三个等腰三角形;③△BCD的周长=AB+BC;④△AMD≌△BCD.其中正确的有A.1个B.2个C.3个D.4个例2.如图,E,F分别是等边三角形ABC的边AB,AC上的点,且BE=AF,CE、BF交于点P(1)求证:CE=BF;(2)求∠BPC的度数.例3.我们把平面内与四边形各边端点构成的三角形都是等腰三角形的点叫做这个四边形的腰点(如矩形的对角线交点是矩形的一个腰点),则正方形的腰点共有_____个.三达标检测1等腰三角形一条边的边长为3,它的另两条边的边长是关于x的一元二次方程x2﹣12x+k=0的两个根,则k的值是()A.27B.36C.27或36D182在△ABC中,AB=AC=10cm,BC=12cm,点D是BC边的中点.点P从点B出发,以每秒1米的速度沿B-A-C的方向运动,设运动时间为T,那么当T=____秒时,过D、P两点的直线将△ABC的周长分成两个部分,使其中一部分是另一部分的2倍。3如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,求证:(1)△ABE≌△DBC(2)△BPQ为等边三角形四拓展提升4如图,抛物线经过的三个顶点,已知轴,点在轴上,点在轴上,且.(1)求抛物线的对称轴;(2)写出三点的坐标并求抛物线的解析式;(3)探究:若点是抛物线对称轴上且在轴下方的动点,是否存在是等腰三角形.若存在,求出所有符合条件的点坐标;不存在,请说明理由.五巩固预习任务布置阅读P37——39平形四边形ACByx011教学反思: