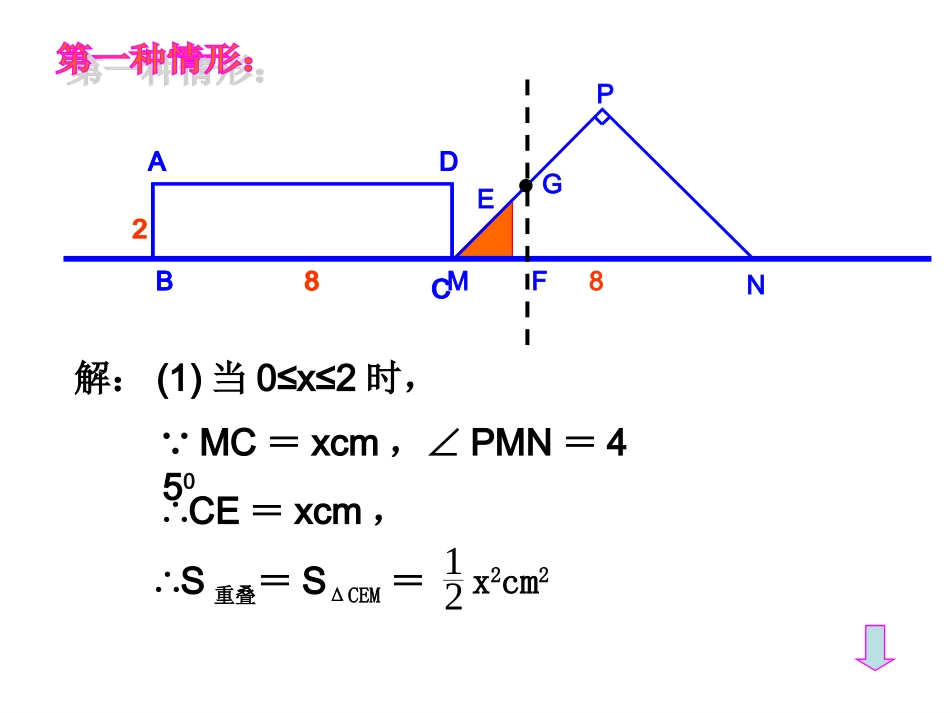
例1、Rt△PMN中,∠P=90°,PM=PN,MN=8cm,矩形ABCD的长和宽分别为8cm和2cm,C点和M点重合,BC和MN在一条直线上。令Rt△PMN不动,矩形ABCD沿MN所在直线向右以每秒1cm的速度移动,直到C点与N点重合为止。设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y,(1)求y与x之间的函数关系式?(2)若重叠部分的面积为等腰直角ΔPMN面积的一半,求x?ABCDMNP828ABCDMNP828ABCD28解:(1)当0≤x≤2时,∵MC=xcm,∠PMN=450∴CE=xcm,∴S重叠=SΔCEM=x2cm221GFEABCDMNP828ABCDGFHT解:(2)当2<x≤6时,∵MC=x,MF=GF=2,∴CF=GD=x-2∴S重叠=S梯形MCDG=(x-2+x)2=2x-221ABCDMNP8ABCDGFHT解:(3)当6<x≤8时,∴S重叠=S五边形GMCQH=S梯形GMNH-SΔQCNQ21=12-(8-x)2∵y=x2,210≤x≤22x-2,2<x≤62112-(8-x)2,6<x≤8(2)若重叠部分的面积为等腰直角ΔPMN面积的一半,求x?则若x2=8,则x=±4,不合题意舍去21MNP8∵SΔPMN=×4×8=1621则若2x-2=8,则x=5,合题意,保留∴当x=5时,重叠部分的面积为RtΔPNN的面积的一半ABCDMNP828例2、菱形OABC的边长为4cm,∠AOC=600,动点P从O出发,以每秒1cm的速度沿OAB路线运动,点P出发2秒后,动点Q从O出发,在OA上以每秒1cm的速度运动,在AB上以每秒2cm的速度沿OAB运动,过P、Q两点分别作对角线AC的平行线,设P点运动的时间为x秒,这两条平行线在菱形上截出的图形的周长为ycm,问当x为多少时,周长y可能为一个定值,定值为多少?BOACPABCOPD解:(1)当0≤x≤2时,∴y=3OP,易证ΔPOD为一等边三角形,=3xABCOPQMN解:(2)当2<x≤4时,y=3OP-OQ=3x-(x-2)=2x+2ABCOPQMN解:(3)当4<x≤6时,y=OC+BC+AQ+AP=4OA-OQ-BP=16-(x-2)-(8-x)=10ABCOPNMQ解:(4)当6<x≤8时,y=NQ+BN+QP=3QB-PB=3[4-2(x-6)]-(8-x)=40-5xy=3x,2x+2,10,40-5x,0≤x≤22<x≤44<x≤66<x≤8∴当4≤x≤6时,周长y是一个定值,定值为10总结:1、分解图形的运动过程,寻找分界;2、采用分类讨论的数学思想,将复杂的运动问题转化为简单的数学问题;